题目内容
16.已知:关于x的方程x2-2(k-2)x+k2-2k-2=0.(1)若这个方程有实数根,求k的取值范围.
(2)若此方程有一个根是1,求k的值.
分析 (1)根据方程有实数根结合根的判别式,即可得出△=-8k+24≥0,解之即可得出k的取值范围;
(2)将x=1代入原方程,解之即可求出k值.
解答 解:(1)∵关于x的方程x2-2(k-2)x+k2-2k-2=0有实数根,
∴△=[-2(k-2)]2-4(k2-2k-2)=-8k+24≥0,
解得:k≤3.
(2)将x=1代入原方程得1-2(k-2)+k2-2k-2=k2-4k+3=(k-1)(k-3)=0,
解得:k1=1,k2=3.
点评 本题考查了根的判别式以及因式分解法解一元二次方程,解题的关键是:(1)根据方程有实数根,找出△=-8k+24≥0;(2)将x=1代入原方程求出k值.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
14.用a,b,c作三角形的三边,其中不能构成直角三角形的是( )
| A. | a=$\sqrt{1}$,b=$\sqrt{2}$,c=$\sqrt{3}$ | B. | a=2,b=3,c=4 | C. | a=12,b=5,c=13 | D. | a=$\sqrt{7}$,b=2,c=$\sqrt{3}$ |
 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数?
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数? 已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC.
已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC. 如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.
如图,矩形ABCD中,AB=4,BC=6,E是BC上一点(不与B、C重合),点P在边CD上运动,M、N分别是AE、PE的中点,线段MN长度的最大值是$\sqrt{13}$.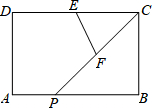 如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.
如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为$\sqrt{2}$+1.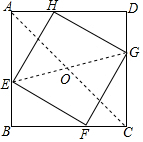 如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.