题目内容
19. 已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,
已知等腰三角形的周长为6cm,底边长y(cm)是腰长x(cm)的函数,(1)写出这个函数的关系式;
(2)求自变量x的取值范围;
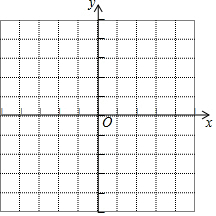
(3)画出函数图象.
分析 (1)根据三角形的周长即可得出2x+y=6,变形后即可得出y=-2x+6;
(2)由三角形的边长大于0,即可得出关于x的一元一次不等式组,解之即可得出自变量x的取值范围;
(3)利用一次函数图象上点的坐标特征,找出一次函数图象上两点的坐标,描点、连线,即可画出函数图象.
解答 解:(1)根据题意得:2x+y=6,
∴y=-2x+6.
(2)∵三角形的边长大于0,
∴$\left\{\begin{array}{l}{x>0}\\{y=-2x+6>0}\end{array}\right.$,
解得:0<x<3.
(3)当x=0时,y=-2x+6=6;
当y=-2x+6=0时,x=3.
描点、连线,画出函数图象,如图所示.
点评 本题考查了一次函数的应用、等腰三角形的性质、三角形的周长以及一次函数的图象,解题的关键是:(1)根据等腰三角形的周长为6,找出y=-2x+6;(2)根据三角形的边长大于0,找出关于x的一元一次不等式组;(3)利用一次函数图象上点的坐标特征,找出函数图象上的两点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.用a,b,c作三角形的三边,其中不能构成直角三角形的是( )
| A. | a=$\sqrt{1}$,b=$\sqrt{2}$,c=$\sqrt{3}$ | B. | a=2,b=3,c=4 | C. | a=12,b=5,c=13 | D. | a=$\sqrt{7}$,b=2,c=$\sqrt{3}$ |
11.(-x)n=-xn(x≠0)成立的条件是( )
| A. | n是正整数 | B. | n是整数 | C. | n是奇数 | D. | n是偶数 |
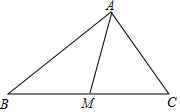 如图,在△ABC中,AM是BC边上的中线,求证:AM<(AB+AC).
如图,在△ABC中,AM是BC边上的中线,求证:AM<(AB+AC).