题目内容
已知函数y=
x2+6x+10.
(1)用配方法把它写成y=a(x-h)2+k的形式;
(2)说出其图象的开口方向、对称轴和顶点坐标;
(3)说出该图象和y=
x2的图象的关系;
(4)画出函数的图象(草图)并回答x为何值时,y<0;x为何值时,y随x增大而减小.
| 1 |
| 2 |
(1)用配方法把它写成y=a(x-h)2+k的形式;
(2)说出其图象的开口方向、对称轴和顶点坐标;
(3)说出该图象和y=
| 1 |
| 2 |
(4)画出函数的图象(草图)并回答x为何值时,y<0;x为何值时,y随x增大而减小.
考点:二次函数的三种形式,二次函数的图象,二次函数的性质
专题:
分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)根据(1)中抛物线的方程可以直接得到答案;
(3)根据抛物线的平移规律进行答题;
(3)根据抛物线开口方向,顶点坐标画出草图.
(2)根据(1)中抛物线的方程可以直接得到答案;
(3)根据抛物线的平移规律进行答题;
(3)根据抛物线开口方向,顶点坐标画出草图.
解答:解:(1)y=
x2+6x+10=
(x2+12x+36)+10-18=
(x+6)2-8.即y=
(x+6)2-8;
(2)由(1)知抛物线的解析式为y=
(x+6)2-8.则该抛物线的对称轴是x=-6,顶点坐标是(-6,-8).
∵
>0,
∴该函数的开口方向向上;
(3)y=
x2的图象先左平移6个单位,再向下平移8个单位,即可得到y=
(x+6)2-8的图象;
(4)由(2)知,抛物线y=
(x+6)2-8的开口方向向上,对称轴是x=-6,顶点坐标是(-6,-8).
∵y=
x2+6x+10=
(x+2)(x+10),
∴该抛物线与x轴的交点坐标是(-2,0),(-10,0).
故其函数图象如图所示:
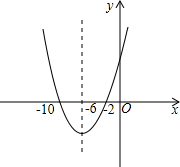 .
.
由图象知,当-10<x<-2时,y<0.
当x<-6时,y随x的增大而减小.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知抛物线的解析式为y=
| 1 |
| 2 |
∵
| 1 |
| 2 |
∴该函数的开口方向向上;
(3)y=
| 1 |
| 2 |
| 1 |
| 2 |
(4)由(2)知,抛物线y=
| 1 |
| 2 |
∵y=
| 1 |
| 2 |
| 1 |
| 2 |
∴该抛物线与x轴的交点坐标是(-2,0),(-10,0).
故其函数图象如图所示:
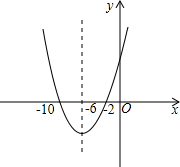 .
.由图象知,当-10<x<-2时,y<0.
当x<-6时,y随x的增大而减小.
点评:本题考查了二次函数的三种形式,二次函数的性质和图象.作出二次函数的草图时,需要得到抛物线与x轴的交点坐标、对称轴直线,顶点坐标以及抛物线的开口方向.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
小李做90个零件与小王做120个零件所用的时间相同,他俩每小时一共做35个零件,设小李每小时做x个零件,则可列方程( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
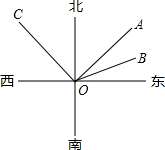 如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得,甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.
如图所示,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A、B、C处时,经测量得,甲船位于港口的北偏东44°方向,乙船位于港口的北偏东76°方向,丙船位于港口的北偏西45°方向.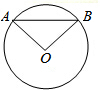 已知:如图,在⊙O中,
已知:如图,在⊙O中,
 如图,在⊙O中,弦AB与CD相交于点F,∠BCD=40°,∠BFD=70°,求∠ADC的度数.
如图,在⊙O中,弦AB与CD相交于点F,∠BCD=40°,∠BFD=70°,求∠ADC的度数. 如图是小明在课堂上画得的一个图形,AB∥CD,他要想得出∠1=∠2,那么还需要添加一个什么条件?请你帮助一下小明,并说明理由.
如图是小明在课堂上画得的一个图形,AB∥CD,他要想得出∠1=∠2,那么还需要添加一个什么条件?请你帮助一下小明,并说明理由.