题目内容
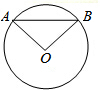 已知:如图,在⊙O中,
已知:如图,在⊙O中, |
| AB |
(1)∠AOB的度数;(精确到1度)
(2)AB的长度;(精确到0.1cm)
(3)△AOB的面积.
考点:弧长的计算,勾股定理,垂径定理
专题:
分析:(1)直接根据弧长公式求出∠AOB的度数即可;
(2)作OD⊥AB,则AD=BD,根据三角函数即可求出AD的长,从而求出AB的长.
(3)求出OD的长,根据三角形的面积公式解答即可.
(2)作OD⊥AB,则AD=BD,根据三角函数即可求出AD的长,从而求出AB的长.
(3)求出OD的长,根据三角形的面积公式解答即可.
解答: 解:(1)∵
解:(1)∵
长为4cm,OA=3cm,
∴
=4,解得n≈76.4°,即∠AOB≈76.4°;
(2)∵∠AOB=76.4°,
∴∠AOD=76.4°×
=38.2°,
∴AD=AO•sin38.2°≈1.854cm,
∴AB≈1.854×2=3.7cm.;
(3)∵OD=AO•sin38.2°≈1.86cm,
∴S△AOB≈
×3.7×1.86≈3.4cm2.
 解:(1)∵
解:(1)∵ |
| AB |
∴
| nπ×3 |
| 180 |
(2)∵∠AOB=76.4°,
∴∠AOD=76.4°×
| 1 |
| 2 |
∴AD=AO•sin38.2°≈1.854cm,
∴AB≈1.854×2=3.7cm.;
(3)∵OD=AO•sin38.2°≈1.86cm,
∴S△AOB≈
| 1 |
| 2 |
点评:本题考查了弧长的计算,涉及勾股定理、三角形的面积、三角函数等知识,解题的关键是能用计算器求出三角函数值.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列各组长度的线段能构成三角形的是( )
| A、1.5cm,3.9cm,2.3cm |
| B、3.5cm,7.1cm,3.6cm |
| C、6cm,1cm,6cm |
| D、4cm,10cm,4cm |
由四舍五入法得到的近似数为8.01×10-4精确到( )
| A、万位 | B、百分位 |
| C、百万分位 | D、百位 |
 如图,一工件的凹面要求做成半圆,如何用一把曲尺(它的角是直角)检查工件的凹面是否符合要求?
如图,一工件的凹面要求做成半圆,如何用一把曲尺(它的角是直角)检查工件的凹面是否符合要求? 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.