题目内容
说出下列二次函数图象的开口方向、顶点坐标、对称轴及函数的最值.
(1)y=3(x-1)2;
(2)y=2(x+1)2;
(3)y=-
(x-4)2+3.
(1)y=3(x-1)2;
(2)y=2(x+1)2;
(3)y=-
| 1 |
| 2 |
考点:二次函数的性质
专题:
分析:分别根据二次函数的顶点式可以得出每个二次函数的开口方向、顶点坐标、对称轴及最值.
解答:解:(1)∵y=3(x-1)2,
∴二次函数图象开口向上,顶点坐标为(1,0),对称轴为x=1,函数有最小值0;
(2)∵y=2(x+1)2,
∴二次函数图象开口向上,顶点坐标为(-1,0),对称轴为x=-1,函数有最小值0;
(3)y=-
(x-4)2+3,
∴二次函数图象开口向下,顶点坐标为(4,0),对称轴为x=4,函数有最大值3.
∴二次函数图象开口向上,顶点坐标为(1,0),对称轴为x=1,函数有最小值0;
(2)∵y=2(x+1)2,
∴二次函数图象开口向上,顶点坐标为(-1,0),对称轴为x=-1,函数有最小值0;
(3)y=-
| 1 |
| 2 |
∴二次函数图象开口向下,顶点坐标为(4,0),对称轴为x=4,函数有最大值3.
点评:本题主要考查二次函数的开口方向、对称轴、顶点坐标及最值,掌握二次函数的开口方程与a的正负有关,在y=a(x-h)2+k中其对称轴为x=h,顶点坐标为(h,k),最值为k是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
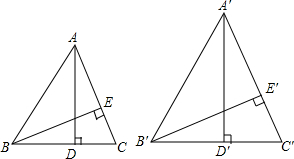 如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证:
如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证: 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起. 如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是
如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是