题目内容
 如图是小明在课堂上画得的一个图形,AB∥CD,他要想得出∠1=∠2,那么还需要添加一个什么条件?请你帮助一下小明,并说明理由.
如图是小明在课堂上画得的一个图形,AB∥CD,他要想得出∠1=∠2,那么还需要添加一个什么条件?请你帮助一下小明,并说明理由.考点:平行线的性质
专题:探究型
分析:由AB∥CD可知∠BAC=∠ACD,要使∠1=∠2成立,需要添一条件为AE∥CF或AB∥EF.
解答:解:需添加的条件为AE∥CF或AB∥EF.
理由(一):∵AB∥CD,
∴∠BAC=∠ACD,
∵AE∥CF,
∴∠EAC=∠FCA,
∴∠1=∠2;
理由(二):∵AB∥CD,AB∥EF,
∴CD∥EF,
∴∠1=∠E,∠E=∠F,∠2=∠F,
∴∠1=∠2.
理由(一):∵AB∥CD,
∴∠BAC=∠ACD,
∵AE∥CF,
∴∠EAC=∠FCA,
∴∠1=∠2;
理由(二):∵AB∥CD,AB∥EF,
∴CD∥EF,
∴∠1=∠E,∠E=∠F,∠2=∠F,
∴∠1=∠2.
点评:本题主要考查了平行线的性质,熟练应用性质是解题的关键.

练习册系列答案
相关题目
由四舍五入法得到的近似数为8.01×10-4精确到( )
| A、万位 | B、百分位 |
| C、百万分位 | D、百位 |
 如图,一工件的凹面要求做成半圆,如何用一把曲尺(它的角是直角)检查工件的凹面是否符合要求?
如图,一工件的凹面要求做成半圆,如何用一把曲尺(它的角是直角)检查工件的凹面是否符合要求?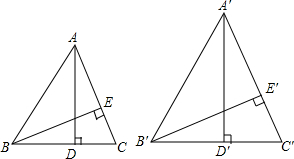 如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证:
如图,△ABC与△A′B′C′相似,AD,BE是△ABC的高,A′D′,B′E′是△A′B′C′的高,求证: 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起. 如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是
如图1,是一个小正方体的表面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是 如图,直线AB、CD相交于点O,OA平分∠COE,∠COE:∠EOD=4:5,求∠BOC的度数.
如图,直线AB、CD相交于点O,OA平分∠COE,∠COE:∠EOD=4:5,求∠BOC的度数.