题目内容
7.在同一直角坐标系中,一次函数y=2x+1与反比例函数y=$\frac{k}{x}$的图象没有交点,则k的取值范围是( )| A. | k>0 | B. | k<0 | C. | k$>-\frac{1}{8}$ | D. | k$<-\frac{1}{8}$ |
分析 一次函数y=2x+1与反比例函数y=$\frac{k}{x}$的图象没有交点,就是两函数解析式所组成的方程组无解,据此即可求得k的范围.
解答 解:根据题意,得$\left\{\begin{array}{l}{y=2x+1}\\{y=\frac{k}{x}}\end{array}\right.$,
整理得2x2+x-k=0,
当两函数图象没有公共点时,△<0,即1+8k<0,
解得k<-$\frac{1}{8}$,
故两函数图象无公共点时k<-$\frac{1}{8}$.
故选D.
点评 本题考查了反比例函数与一次函数的交点问题.关键是根据形数结合,判断无交点时,图象的位置与系数的关系,找出只有一个交点时k的值,再确定k的取值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.如果关于x的方程(m+2)x2-2(m+1)x+m=0有且只有一个实数根,那么关于x的方程(m+1)x2-2mx+m-1=0的根为( )
| A. | -1或-3 | B. | 1或3 | C. | -1或3 | D. | 1或-3 |
15.若一个多边形的内角和为900°,则从这个多边形的其中一个顶点出发引的对角线的条数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
2.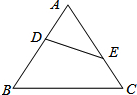 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
 如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )
如图,在△ABC中,已知∠AED=∠B,DE=6;AB=10,AE=5,则BC的长为( )| A. | 3 | B. | 12 | C. | $\frac{25}{3}$ | D. | 7 |
 如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒.
如图,B是线段AD上一动点,沿A→D以2cm/s的速度运动,C是线段BD的中点,AD=10cm,设点B运动时间为t秒. 如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.
如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.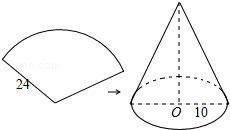 如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是240πcm2.
如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是240πcm2.