题目内容
10.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”,如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”.(1)52和2015这两个数是“神秘数”吗?为什么?
(2)设两个连续的偶数为2k和2k+2(其中k为非负数),由这两个连续偶数构造的“神秘数”是4的倍数吗?为什么?
(3)两个连续奇数的平方差(k取正数)是“神秘数”吗?为什么?
分析 (1)根据相邻两个偶数的平方差,可得答案;
(2)根据相邻两个偶数的平方差,神秘数的定义,可得答案;
(3)根据相邻两个奇数的平方差,神秘数的定义,可得答案.
解答 解:(1)设(2k+2)2-(2k)2=52,解得k=6,
52是神秘数;
(2k+2)2-(2k)2=2015,
解得k=$\frac{2011}{8}$,
2015不是神秘数;
(2)两个连续的偶数为2k和2k+2(其中k为非负数),由这两个连续偶数构造的“神秘数”是4的倍数,
理由如下:
(2k+2)2-(2k)2=8k+4=4(2k+1),
两个连续的偶数为2k和2k+2(其中k为非负数),由这两个连续偶数构造的“神秘数”是4的倍数;
(3)两个连续奇数的平方差(k取正数)不是“神秘数”,理由如下:
(2k+1)2-(2k-1)2=8k,又神秘数为4的倍数,而不是8的倍数;
故两个连续奇数的平方差(k取正数)不是“神秘数”.
点评 本题考查了平方差公式,利用平方差公式是解题关键.

练习册系列答案
相关题目
15.根据等式的性质,下列各式变形正确的是( )
| A. | 由$\frac{x}{5}$=20得x=4 | B. | 由3x-2=2x+2得x=4 | ||
| C. | 由2x-3=3x得x=3 | D. | 由3x-5=7得3x=7-5 |
 如图所示,点A、B在数轴上,AB=6,点A对应的数为-1,则点B对应的数为5.
如图所示,点A、B在数轴上,AB=6,点A对应的数为-1,则点B对应的数为5.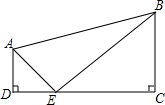 如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?
如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?