题目内容
18.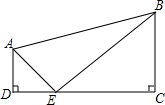 如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?
如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?
分析 设DE的长为x,分两种情况:①当$\frac{DE}{BC}=\frac{AD}{CE}$时,得出方程,解方程即可;②当$\frac{DE}{CE}=\frac{AD}{BC}$时,得出方程,解方程即可.
解答 解:设DE的长为x,则CE=7-x,
∵∠D=∠C=90°,
∴分两种情况,
①当$\frac{DE}{BC}=\frac{AD}{CE}$时,
即$\frac{x}{3}=\frac{2}{7-x}$,
解得:x=1,或x=6;
②当$\frac{DE}{CE}=\frac{AD}{BC}$时,
即$\frac{x}{7-x}=\frac{2}{3}$,
解得:x=$\frac{14}{5}$;
综上所述:当DE为1或6或$\frac{14}{5}$时,△EAD与△EBC相似.
点评 本题考查了相似三角形的判定方法、解方程;熟练掌握相似三角形的判定方法,由两边成比例得出方程是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
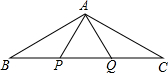 P、Q是△ABC的边BC上两点,且BP=QC=AP=AQ.
P、Q是△ABC的边BC上两点,且BP=QC=AP=AQ.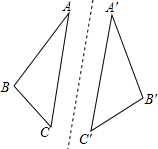 如图,△ABC与△A′B′C′关于直线l对称,对应线段AB和A′B′所在的直线相交吗?另外两组对应线段所在的直线相交吗?如果相交,交点与对称轴l有什么关系?如果不相交,这组对应线段所在直线与对称轴l有什么关系?再找几个成轴对称的图形观察一下,你能发现什么规律?
如图,△ABC与△A′B′C′关于直线l对称,对应线段AB和A′B′所在的直线相交吗?另外两组对应线段所在的直线相交吗?如果相交,交点与对称轴l有什么关系?如果不相交,这组对应线段所在直线与对称轴l有什么关系?再找几个成轴对称的图形观察一下,你能发现什么规律?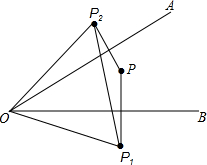 如图,已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称.求证:点P1,O,P2三点所构成的三角形是等边三角形.
如图,已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称.求证:点P1,O,P2三点所构成的三角形是等边三角形.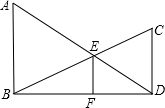 如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1.
如图,AB⊥BD,CD⊥BD,B、D是垂足,AD和BC交于E,EF⊥BD于F.求证:$\frac{DE}{AD}$+$\frac{BE}{BC}$=1. 如图,矩形ABCD中,AB:BC=$\sqrt{2}$:1,把矩形ABCD沿EF对折,请你判断矩形AEFD与矩形ABCD相似吗?为什么?
如图,矩形ABCD中,AB:BC=$\sqrt{2}$:1,把矩形ABCD沿EF对折,请你判断矩形AEFD与矩形ABCD相似吗?为什么?