题目内容
6.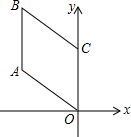 如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )| A. | (-2,2+$\sqrt{2}$) | B. | (2,2+$\sqrt{2}$) | C. | ($-\sqrt{2}$,2+$\sqrt{2}$) | D. | ($\sqrt{2}$,2+$\sqrt{2}$) |
分析 作BF⊥y轴于F,则∠BFC=90°,由菱形的性质得出OC=OA=CB=2,BC∥OA,得出∠BCF=∠AOC=45°,△BCF是等腰直角三角形,根据三角函数求出BF=CF,得出OF,即可得出B点坐标.
解答 解:作BF⊥y轴于F,如图所示: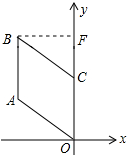 则∠BFC=90°,
则∠BFC=90°,
∵四边形OABC是菱形,
∴OC=OA=CB=2,BC∥OA,
∴∠BCF=∠AOC=45°,
∴△BCF是等腰直角三角形,
∴BF=CF=BC×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
∴OF=2+$\sqrt{2}$,
∴B点的坐标是:(-$\sqrt{2}$,2+$\sqrt{2}$);
故选:C.
点评 本题考查了菱形的性质、坐标与图形特征、等腰直角三角形的判定与性质、三角函数;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
17.下列结论正确的是( )
| A. | 同位角相等 | |
| B. | 垂直于同一直线的两条直线互相平行 | |
| C. | 过一点有且只有一条直线与这条直线平行 | |
| D. | 同一平面内,不相交的两条直线叫做平行线 |
11. 南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:
频数分布表
(2)结合整理的数据完成频数分布直方图,通过观察直方图你可以得到哪些信息?请你写出你得到的信息.
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
 南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
(1)请你将调查数据进行如下整理:
频数分布表
| 分组 | 划记(用正字划记) | 频数 |
| 2.0<x≤3.5 | ||
| 3.5<x≤5.0 | ||
| 5.0<x≤6.5 | ||
| 6.5<x≤8.0 | ||
| 8.0<x≤9.5 | ||
| 合计 |
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定多少吨?
16.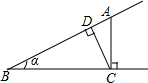 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )| A. | $\frac{BD}{BC}$ | B. | $\frac{BC}{AB}$ | C. | $\frac{AD}{AC}$ | D. | $\frac{CD}{AC}$ |
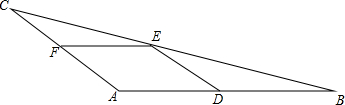 如图,△ABC中,D、E、F分别是AB、BC、AC上的点,四边形ADEF是菱形,AB=15,AC=10,则菱形的周长是( )
如图,△ABC中,D、E、F分别是AB、BC、AC上的点,四边形ADEF是菱形,AB=15,AC=10,则菱形的周长是( )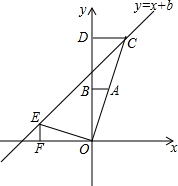 如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).
如图,在平面直角坐标系中,点O是坐标原点,Rt△OAB的直角顶点B在y轴的正半轴上,以原点O为位似中心,位似比为2:1,把△OAB放大,放大后的三角形为△OCD,把△OAB绕点O逆时针旋转90°后得△OEF,点A的坐标是(1,t).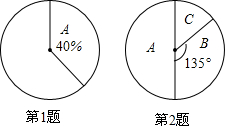 根据扇形统计图,解决下列问题:
根据扇形统计图,解决下列问题: