题目内容
18.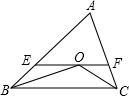 △ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
△ABC中,∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.(1)求证:OE=BE;
(2)若△ABC的周长比△AEF的周长大10,试求出BC的长度.
分析 (1)由等腰三角形的性质得到∠ABC=∠ACB,根据平行线的性质得到∠AEF=∠ABC,等量代换得到∠AEF=∠AFE,根据平行线的性质得到∠EDB=∠DBC,根据角平分线的定义得到∠EBD=∠DBC,于是得到结论;
(2)根据等腰三角形的性质和三角形的周长的计算公式即可得到结论.
解答 解:(1)∵AB=AC,
∴∠ABC=∠ACB,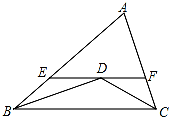
∵EF∥BC,
∴∠AEF=∠ABC,
∴∠AEF=∠AFE,
∵EF∥BC,
∴∠EDB=∠DBC,
∵∠ABC和∠ACB的平分线交于点D,
∴∠EBD=∠DBC,
∴∠EBD=∠EDB,
∵∠ABC=∠ACB,
∴∠DBC=∠DCB,
∴BE=DE;
(2)由(1)证得BE=DE,
同理DF=CF,
∴△AEF的周长=AB+AC,
∵△ABC的周长比△AEF的周长大10,
∴BC=AB+AC+BC-AB+AC=10.
点评 本题考查了等腰三角形的性质和判定,平行线的性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.已知点A(-4,y1),B(2,y2)都在双曲线y=$\frac{k}{x}$(k>0)上,则y1、y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
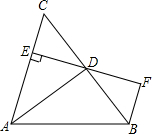 如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为点E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF. 如图,已知线段a,h(a>h),求作等腰三角形ABC,使AB=AC=a,底边BC上的高AD=h(保留作图痕迹,不要求写出作法).
如图,已知线段a,h(a>h),求作等腰三角形ABC,使AB=AC=a,底边BC上的高AD=h(保留作图痕迹,不要求写出作法).