题目内容
 如图,已知菱形ABCD的周长是4cm,∠ABC=120°.
如图,已知菱形ABCD的周长是4cm,∠ABC=120°.①求对角线BD和AC的长.
②求菱形的面积.
考点:菱形的性质
专题:
分析:①求出菱形的边长AB=1cm,再根据菱形的对角线平分一组对角线求出∠ABO=60°,然后根据直角三角形两锐角互余求出∠BAO=30°,再根据直角三角形30°角所对的直角边等于斜边的一半求出BO,利用勾股定理列式求出AO,然后根据菱形的对角线互相平分解答;
②根据菱形的面积等于对角线乘积的一半列式计算即可得解.
②根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解答:解:①∵菱形ABCD的周长是4cm,
∴AB=
×4=1cm,
∵∠ABC=120°,
∴∠ABO=
×120°=60°,
∵菱形的对角线AC⊥BD,
∴∠BAO=90°-60°=30°,
∴BO=
AB=
,
由勾股定理得,AO=
=
=
,
∴BD=2BO=1cm,
AC=2AO=
cm;
②菱形的面积=
AC•BD=
×
×1=
cm2.
∴AB=
| 1 |
| 4 |
∵∠ABC=120°,
∴∠ABO=
| 1 |
| 2 |
∵菱形的对角线AC⊥BD,
∴∠BAO=90°-60°=30°,
∴BO=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,AO=
| AB2-BO2 |
12-(
|
| ||
| 2 |
∴BD=2BO=1cm,
AC=2AO=
| 3 |
②菱形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查了菱形的性质,主要利用了菱形的对角线互相垂直平分的性质,勾股定理,直角三角形30°角所对的直角边等于斜边的一半以及菱形的面积的求解.

练习册系列答案
相关题目
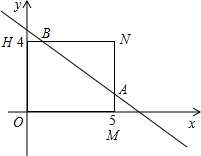 已知一动点P(x,y)在矩形OMNH内随机运动,其中O(0,0),M(5,0),N(5,4),H(0,4),直线y=-
已知一动点P(x,y)在矩形OMNH内随机运动,其中O(0,0),M(5,0),N(5,4),H(0,4),直线y=-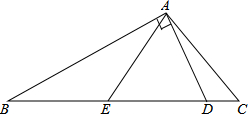 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.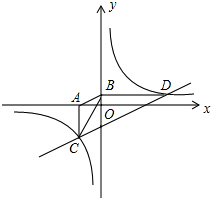 如图,已知双曲线y=
如图,已知双曲线y=