题目内容
若x、y为实数，满足2x-2x2y2-2y（x+x2）-x2=5，则x= ，y= ．
考点：根的判别式
专题：
分析：先将方程进行整理，再利用判别式为0，求出x，再代入方程，即可求出y的值．
解答：解：∵2x-2x2y2-2y（x+x2）-x2=5，
∴-2x2y2-2y（x+x2）-x2+2x-5=0，
∴△=4（x+x2）2+8x2（-x2+2x-5）=0，
∴x=0或x=3，
x=0时，方程不成立，
x=3时，方程为9y2+12y+4=0，
解得：y=-
；
故答案为：3，-
．
∴-2x2y2-2y（x+x2）-x2+2x-5=0，
∴△=4（x+x2）2+8x2（-x2+2x-5）=0，
∴x=0或x=3，
x=0时，方程不成立，
x=3时，方程为9y2+12y+4=0，
解得：y=-
| 2 |
| 3 |
故答案为：3，-
| 2 |
| 3 |
点评：本题考查了根的判别式，把给出的方程通过整理，利用判别式为0，求出x的值是本题的关键．
练习册系列答案
相关题目
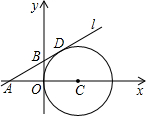如图，在平面直角坐标系中，⊙C与y轴相切，且C点坐标为（1，0），直线l过点A（-1，0），与⊙C相切于点D，求：
如图，已知菱形ABCD的周长是4cm，∠ABC=120°．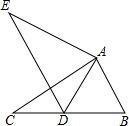
如图，在△ABC中，AB=2，BC=3.8，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为