题目内容
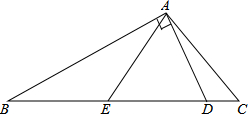 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE.(1)求证:∠AEC=∠C;
(2)求证:BD=2AC.
考点:等腰三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)在Rt△ADB中,点E是BD的中点;根据直角三角形的性质,可得BE=AE,故∠AEC=2∠B=∠C;
(2)同(1),可得BD=2AE,再根据(1)的结论可得AE=AC,代换可得结论.
(2)同(1),可得BD=2AE,再根据(1)的结论可得AE=AC,代换可得结论.
解答:(1)证明:∵AD⊥AB,
∴△ABD为直角三角形,
又∵点E是BD的中点,
∴AE=
BD,
又∵BE=
BD,
∴AE=BE,
∴∠B=∠BAE,
又∵∠AEC=∠B+∠BAE,
∴∠AEC=∠B+∠B=2∠B,
又∵∠C=2∠B,
∴∠AEC=∠C.
(2)证明:∵∠AEC=∠C,
∴AE=AC,
又∵AE=
BD,
∴BD=2AE,
∴BD=2AC.
∴△ABD为直角三角形,
又∵点E是BD的中点,
∴AE=
| 1 |
| 2 |
又∵BE=
| 1 |
| 2 |
∴AE=BE,
∴∠B=∠BAE,
又∵∠AEC=∠B+∠BAE,
∴∠AEC=∠B+∠B=2∠B,
又∵∠C=2∠B,
∴∠AEC=∠C.
(2)证明:∵∠AEC=∠C,
∴AE=AC,
又∵AE=
| 1 |
| 2 |
∴BD=2AE,
∴BD=2AC.
点评:本题考查直角三角形的有关性质、三角形的外角性质,等腰三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
一条直线y=kx+b其中k+b=-6,kb=8,那么该直线经过( )
| A、第二、四象限 |
| B、第一、二、三象限 |
| C、第一、三象限 |
| D、第二、三、四象限 |
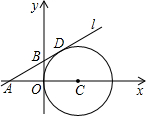 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求:
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线l过点A(-1,0),与⊙C相切于点D,求: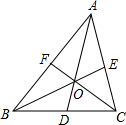 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长. 如图,已知菱形ABCD的周长是4cm,∠ABC=120°.
如图,已知菱形ABCD的周长是4cm,∠ABC=120°.