题目内容
我市某化工厂现库存A、B两种原料502kg,且已知B原料比A原料少78kg.计划用这两种原料生产甲、乙两种产品共80件,已知生产一件甲种产品需要A种原料5kg和B种原料1.5kg;生产一件乙种产品需要A种原料2.5kg和B种原料3.5kg.请解决下列问题:
(1)求库存的A、B两种原料各是多少kg?
(2)根据题意设计出甲、乙种产品的生产方案.
(3)若生产一件甲种产品可获利润1000元,生产一件乙种产品可获利1500元,那么在(2)中哪种方案获利润最大?最大利润是多少元?
(1)求库存的A、B两种原料各是多少kg?
(2)根据题意设计出甲、乙种产品的生产方案.
(3)若生产一件甲种产品可获利润1000元,生产一件乙种产品可获利1500元,那么在(2)中哪种方案获利润最大?最大利润是多少元?
考点:一元一次方程的应用
专题:
分析:(1)设库存的A种原料xkg,则库存的B种原料(x-78)kg,根据两种原料的库存量为502kg建立方程求出其解即可;
(2)根据(1)的结论,设生产甲产品a件,则生产乙产品(80-a)件,根据两种原材料的关系建立方程组求出其解即可;
(3)设生产两种产品的总利润为W元,由销售问题的数量关系建立W与x的解析式即可.
(2)根据(1)的结论,设生产甲产品a件,则生产乙产品(80-a)件,根据两种原材料的关系建立方程组求出其解即可;
(3)设生产两种产品的总利润为W元,由销售问题的数量关系建立W与x的解析式即可.
解答:解:(1)设库存的A种原料xkg,则库存的B种原料(x-78)kg,由题意,得
x+(x-78)=502,
解得:x=290,
∴B种原料为:502-290=212kg.
答:库存的A种原料290kg,则库存的B种原料212kg;
(2)设生产甲产品a件,则生产乙产品(80-a)件,由题意,得
,
解得:34≤a≤36.
∵a为整数,
∴a=34,35,36.
方案1,甲产品34件,生产乙产品46件;
方案2,甲产品35件,生产乙产品45件;
方案3,甲产品36件,生产乙产品44件.
(3)设生产两种产品的总利润为W元,由题意,得
W=1000a+1500(80-a)=-500a+120000,
∴k=-500<0,
∴W随a的增大而减小,
∴当a=34时.W最大=103000元.
方案1,甲产品34件,生产乙产品46件利润最大为103000元.
x+(x-78)=502,
解得:x=290,
∴B种原料为:502-290=212kg.
答:库存的A种原料290kg,则库存的B种原料212kg;
(2)设生产甲产品a件,则生产乙产品(80-a)件,由题意,得
|
解得:34≤a≤36.
∵a为整数,
∴a=34,35,36.
方案1,甲产品34件,生产乙产品46件;
方案2,甲产品35件,生产乙产品45件;
方案3,甲产品36件,生产乙产品44件.
(3)设生产两种产品的总利润为W元,由题意,得
W=1000a+1500(80-a)=-500a+120000,
∴k=-500<0,
∴W随a的增大而减小,
∴当a=34时.W最大=103000元.
方案1,甲产品34件,生产乙产品46件利润最大为103000元.
点评:本题考查了列一元一次方程解实际问题的运用,一元一次不等式组解实际问题的运用,一次函数的解析式的性质的运用,解答时求互一次函数的解析式是关键.

练习册系列答案
相关题目

 请写出点A,B,C,D,的坐标.
请写出点A,B,C,D,的坐标. 如图,已知菱形ABCD的周长是4cm,∠ABC=120°.
如图,已知菱形ABCD的周长是4cm,∠ABC=120°. 如图,EF∥AD,∠1=∠2.求证:DG∥AB.
如图,EF∥AD,∠1=∠2.求证:DG∥AB.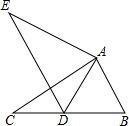 如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
如图,在△ABC中,AB=2,BC=3.8,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为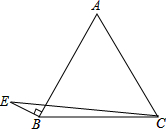 如图,已知:等边△ABC,AB=2
如图,已知:等边△ABC,AB=2