题目内容
19. 如图,在△ABD中,∠D=90°,C是BD上一点,已知BC=9,AB=17,AC=10,求AD的长.
如图,在△ABD中,∠D=90°,C是BD上一点,已知BC=9,AB=17,AC=10,求AD的长.
分析 在Rt△ABD和Rt△ACD中,利用勾股定理列式表示出CD,然后解方程即可.
解答 解:在Rt△ABD中,9+CD=$\sqrt{1{7}^{2}-A{D}^{2}}$,
和Rt△ACD中,CD=$\sqrt{1{0}^{2}-A{D}^{2}}$,
∴9+$\sqrt{1{0}^{2}-A{D}^{2}}$=$\sqrt{1{7}^{2}-A{D}^{2}}$,
两边平方得,81+18$\sqrt{1{0}^{2}-A{D}^{2}}$+100-AD2=289-AD2,
∴$\sqrt{1{0}^{2}-A{D}^{2}}$=6,
两边平方得,100-AD2=36,
解得AD=8.
点评 本题考查了勾股定理,在两个直角三角形中列式表示出CD是解题的关键,要注意无理方程的求解技巧.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.方程(x-1)(x-3)=2的根是( )
| A. | x1=1,x2=3 | B. | x=2±2$\sqrt{3}$ | C. | x=2±$\sqrt{3}$ | D. | x=-2±2$\sqrt{3}$ |
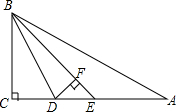 如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.
如图,在直角三角形ABC中,∠C=90°,BD是△ABC的角平分线,BE是△BDA的角平分线,DF是△BDE的高线,已知∠DBE=15°,求∠A和∠EDF的度数.