Question

14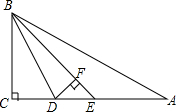．如图，在直角三角形ABC中，∠C=90°，BD是△ABC的角平分线，BE是△BDA的角平分线，DF是△BDE的高线，已知∠DBE=15°，求∠A和∠EDF的度数．

Answer 1

分析 根据三角形的角平分线的定义即可求解∠ABE以及∠ABC的度数，在△ABC中利用三角形内角和定理求得∠A的度数，然后利用三角形外角的性质求得∠DEF，进而求得∠EDF的度数．

解答 解：∵BE是△BDA的角平分线，
∴∠ABE=∠DBE=15°，∠ABD=30°，
∵BD是△ABC的角平分线，
∴∠CBD=∠ABD=30°，∠ABC=60°，
∴在直角△ABC中，∠A=90°-∠ABC=90°-60°=30°，
在△ABE中，∠DEF=∠A+∠ABE=30°+15°=45°，
在直角△DEF中，∠EDF=90°-∠DEF=90°-45°=45°．

点评 本题考查了三角形的角平分线的定义以及三角形的内角和定理，正确利用角平分线的定义求得∠ABC的度数是关键．