题目内容
10.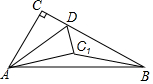 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.
分析 先根据∠ACB=90°,∠ABC=30°,AB=6,求得AC=$\frac{1}{2}$AB=3,BC=$\sqrt{3}$AC=3$\sqrt{3}$,再根据AC1+BC1≥AB,即可得到3+BC1≥6,即BC1≥3,进而得到BC1的最小值为3,再根据当点D与点B重合时,BC1的长最大,得出BC1=BC=3$\sqrt{3}$,最后根据3≤BC1≤3$\sqrt{3}$,即可得出BC1可能的整数值.
解答 解:∵∠ACB=90°,∠ABC=30°,AB=6,
∴AC=$\frac{1}{2}$AB=3,BC=$\sqrt{3}$AC=3$\sqrt{3}$,
由折叠可得AC=AC1=3,
∵AC1+BC1≥AB,
∴3+BC1≥6,即BC1≥3,
如图所示,当点C1落在AB上时,BC1的最小值为3,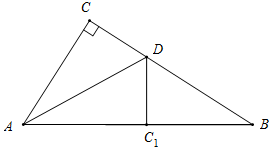
如图所示,当点D与点B重合时,BC1的长最大,
此时BC1=BC=3$\sqrt{3}$,即BC1最大值为3$\sqrt{3}$,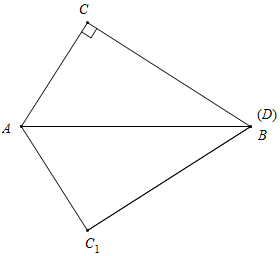
综上所述,3≤BC1≤3$\sqrt{3}$,
∴BC1可能的整数值为3,4,5.
故答案为:3,4,5.
点评 本题主要考查了折叠问题以及含30°角的直角三角形的性质的运用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;翻折变换(折叠问题)实质上就是轴对称变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在数学课上,老师提出如下问题:
小云的作法如下:
小云作图的依据是四条边相等的四边形为菱形,菱形的对边平行.
尺规作图:过直线外一点作已知直线的平行线. 已知:直线l及其外一点A. 求作:l的平行线,使它经过点A. |
| (1)在直线l上任取一点B; (2)以B为圆心,BA长为半径作弧,交直线l于点C; 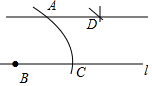 (3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D; (4)作直线AD. 直线AD即为所求. |
2.下列一元二次方程没有实数根的是( )
| A. | x2-2x-1=0 | B. | x2+x+3=0 | C. | x2-1=0 | D. | x2+2x+1=0 |
19.如果a+b=3,则代数式$\frac{{a}^{2}-{b}^{2}}{a}$÷$\frac{a-b}{2a}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | 3 | D. | 6 |
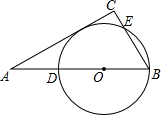 如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.
如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.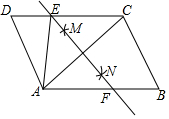 如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.
如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.