题目内容
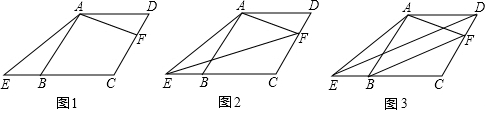
20.如图,菱形ABCD中,∠ABC=60°,E是射线CB上一点,F是CD上一点,且∠EAF=120°.(1)如图1,求证:$\frac{AE}{AF}$=$\frac{AB}{CF}$;
(2)如图2,若△CEF的面积为2$\sqrt{3}$,求AB的长;
(3)如图3,求证:BF∥DE.
分析 (1)如图1,连接AC,根据菱形的性质得到∠D=60°,推出△ACB是等边三角形,求得∠BAC=60°根据相似三角形的性质得到$\frac{AE}{AF}=\frac{AC}{CF}$,等量代换得到结论;
(2)过F作FM⊥CE于M交EC的延长线于M,可得FM=$\frac{\sqrt{3}}{2}$CF,根据三角形的面积列方程得到CE•CF=8,于是得到结论;
(3)由(1)有$\frac{AC}{CF}$=$\frac{CE}{AC}$,求得$\frac{CF}{CD}$=$\frac{CB}{CE}$,根据相似三角形的性质得到∠CBF=∠CED,即可得到结论.
解答 
 解:(1)如图1,连接AC,
解:(1)如图1,连接AC,
∵在菱形ABCD中,∠ABC=60°,
∴∠D=60°,△ACB是等边三角形,
∴∠BAC=60°,
∵∠EAF=120°,
∴∠EAB=∠DAF,
∵∠EAC=60°+∠EAB,∠AFC=60°+∠DAF,
∴∠EAC=∠AFC,
∵∠ACE=∠ACF=60°,
∴△ACE∽△CAF,
∴$\frac{AE}{AF}=\frac{AC}{CF}$,
∵AB=AC,
∴$\frac{AE}{AF}$=$\frac{AB}{CF}$;
(2)由(1)知$\frac{AC}{CF}$=$\frac{CE}{AC}$,
∴AC2=CE•CF,
如图2,过F作FM⊥CE于M交EC的延长线于M,
可得FM=$\frac{\sqrt{3}}{2}$CF,
∵△CEF的面积为2$\sqrt{3}$,
即$\frac{1}{2}$CE•FM=$\frac{1}{2}$CE•$\frac{\sqrt{3}}{2}$CF=2$\sqrt{3}$,
∴CE•CF=8,
即AC2=AB2=8,
∴AB=2$\sqrt{2}$;
(3)由(1)有$\frac{AC}{CF}$=$\frac{CE}{AC}$,
易知AC=AB=BC=CD,
∴$\frac{CD}{CF}$=$\frac{CE}{BC}$,
即$\frac{CF}{CD}$=$\frac{CB}{CE}$,
∵∠BCF=∠ECD,
∴△CBF∽△CED,
∴∠CBF=∠CED,
∴BF∥ED.
点评 本题考查了菱形的性质,相似三角形的判定和性质,平行线的判定,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案| 起步价:3公里以内9元(不再收取燃油附加税) 每公里价格:超过3公里部分,2元/公里(不足1公里按1公里算) 空驶补贴费:超过12公里以上部分,每公里加收公里运价的50% |
(2)有同事告诉他,可以考虑中途到12公里时下车换乘出租车,节省费用,他试了一下,发现换乘车后第二次距离大于3公里,但未超过12公里,而且他还发现比之前不换车总费用少2元,请你算算他的工作单位离家的距离.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 下列俯视图正确的是( )
下列俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
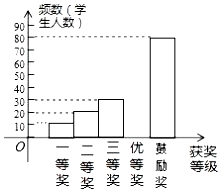 为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
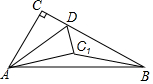 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.