题目内容
12.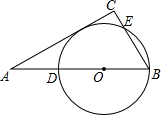 如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.
如图,在△ACB中,∠C=90°,AB=2BC,点O在边AB上,且BO=$\frac{1}{3}$AB,以O为圆心,OB长为半径的圆分别交AB,BC于D,E两点.(1)求证:AC是⊙O的切线;
(2)判断由D,O,E及切点所构成的四边形的形状,并说明理由.
分析 (1)作OF⊥AC于F,如图,理由三角函数可得到∠A=30°,则OA=2OF,再利用BO=$\frac{1}{3}$AB得到OA=2OB,所以OF=OB,于是根据切线的判定方法可判定AC是⊙O的切线;
(2)先证明△OFD和△OBE都是等边三角形得到OD=DF,∠BOE=60°,则可计算出∠EOF=60°,从而可判定△OEF为等边三角形,所以EF=OE,则有OD=DF=EF=OE,然后根据菱形的判定方法可判断四边形ODFE为菱形.
解答 (1)证明: 作OF⊥AC于F,如图,
作OF⊥AC于F,如图,
∵∠C=90°,AB=2BC,
∴sinA=$\frac{BC}{AB}$=$\frac{1}{2}$,
∴∠A=30°,
∴OA=2OF,
∵BO=$\frac{1}{3}$AB,
∴OA=2OB,
∴OF=OB,
∴AC是⊙O的切线;
(2)四边形ODFE为菱形.理由如下:
∵∠A=30°,
∴∠AOF=∠B=60°,
∴△OFD和△OBE都是等边三角形,
∴OD=DF,∠BOE=60°,
∴∠EOF=180°-60°-60°=60°,
∴△OEF为等边三角形,
∴EF=OE,
∴OD=DF=EF=OE,
∴四边形ODFE为菱形.
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.要判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”.也考查了等边三角形的判定与性质和菱形的判定方法.

练习册系列答案
相关题目
2.若分式$\frac{x-1}{x-2}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x=2 | C. | x≠2 | D. | x>2 |
3. 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )
 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )| A. | ∠A=∠ABE | B. | ∠A=∠EBD | C. | ∠C=∠ABC | D. | ∠C=∠ABE |
20.若x=1是方程ax2+bx-2=0的一个根,则a+b的值是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
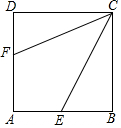 如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.
如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.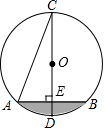 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,.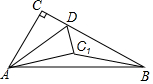 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在C1处,连接C1B,则BC1可能的整数值为3,4,5.