题目内容
2. 如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5.
如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5.
分析 根据菱形的对角相等判断出点E在AB上,点F在CD上,然后根据AB的长度判断出AP的最小值和最大值,写出AP的取值范围即可.
解答 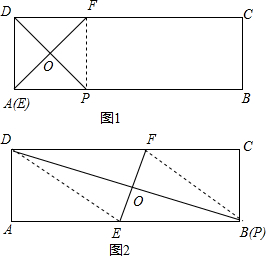 解:∵要使四边形EPFD为菱形,则需DE=EP=FP=DF,
解:∵要使四边形EPFD为菱形,则需DE=EP=FP=DF,
∴如图1:当点E与点A重合时,AP=AD=2,此时AP最小;
如图2:当点P与B重合时,AP=AB=5,此时AP最大;
∴四边形EPFD为菱形的x的取值范围是:2≤x≤5.
故答案为:2≤x≤5.
点评 此题考查了菱形的判定与性质、折叠的性质以及矩形的性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{6}$=3 | B. | $\sqrt{2}$×$\sqrt{6}$=3$\sqrt{2}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | ($\sqrt{12}$-$\sqrt{3}$)×$\sqrt{3}$=3 |
14.下列关于x的方程中,是分式方程的是( )
| A. | 3x=$\frac{1}{2}$ | B. | $\frac{x+2}{5}$=$\frac{3+x}{4}$ | C. | $\frac{1}{x}$=2 | D. | 3x-2y=1 |
12.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a元计算,那么共需要资金( )
| A. | 600a元 | B. | 50a元 | C. | 1200a元 | D. | 1500a元 |
 如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形.
如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形.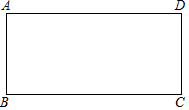 如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.
如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.