题目内容
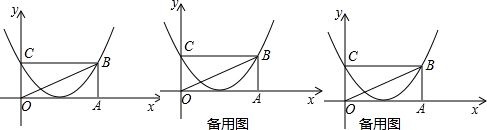
如图,在平面直角坐标系中,点O是坐标原点,抛物线y=
x2+bx+c与y轴相交于C点,过C点作CB∥x轴交抛物线于B点,过B点作BA⊥x轴,垂足为A,连接BO,B点坐标为(4
,4)
(1)求抛物线的解析式;
(2)P点从B点出发以每秒2个单位的速度沿BA向终点A运动,过P点作PQ∥OB交抛物线于Q,设P点运动时间为t秒,当△PBQ为等腰三角形时,求t的值;
(3)在(2)条件下,延长BQ交BQ交x轴于E点,F点在线段OC上,连接EF,过O点作OG⊥EF,垂足为G,连接CG,设F点的纵坐标为m,当线段CG最短时,求m的值,并判断G点是否在(1)中的抛物线上.
| 1 |
| 3 |
| 3 |
(1)求抛物线的解析式;
(2)P点从B点出发以每秒2个单位的速度沿BA向终点A运动,过P点作PQ∥OB交抛物线于Q,设P点运动时间为t秒,当△PBQ为等腰三角形时,求t的值;
(3)在(2)条件下,延长BQ交BQ交x轴于E点,F点在线段OC上,连接EF,过O点作OG⊥EF,垂足为G,连接CG,设F点的纵坐标为m,当线段CG最短时,求m的值,并判断G点是否在(1)中的抛物线上.

考点:二次函数综合题
专题:
分析:(1)根据B的坐标可求得C的坐标,然后根据待定系数法即可求得解析式;
(2)根据tan∠ABO=
=
求得∠ABO=60°,由PQ∥OB,PB=PQ得出∠PBQ=∠PQB=∠OBQ=30°,根据直角三角函数求得PH=t,QH=
t,进而求得QK=4-3t,OK=4
-
t,得出Q(4
-
t,4-3t),代入抛物线的解析式即可求得.
(3)先通过解直角三角形求得OE的长,得出E点的坐标,因为CG+GM≥CM,所以当G在CM上时CG最短,然后根据
=
=
,设GN=
k,得出G(
k,4-3k),分别表示出MR、RG、MG的长,最后根据勾股定理即可求得;
(2)根据tan∠ABO=
| OA |
| AB |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(3)先通过解直角三角形求得OE的长,得出E点的坐标,因为CG+GM≥CM,所以当G在CM上时CG最短,然后根据
| OM |
| OC |
| NG |
| CN |
| ||
| 3 |
| 3 |
| 3 |
解答: 解:(1)如图1,在四边形ABCO中,
解:(1)如图1,在四边形ABCO中,
∵BA⊥x轴,
∴∠BAO=90°,
∵BC∥x轴,
∴∠ABC=∠BAO=90°,
∴四边形ABCD是矩形,
∴AB=OC=4,BC=OA=4
,
∴点C的坐标为(0,4),
依题意可得:
解得
∴所求抛物线的解析式为y=
x2-
x+4;
(2)如图1,过Q作x轴垂线,垂足为K,QH⊥AB,垂足为H.
在RT△ABO中,tan∠ABO=
=
=tan60°,
∴∠ABO=60°,
∵PQ∥OB,
∴∠QPA=∠ABO=60°
∴∠QPB=180°-60°=120°,
∵PB=PQ=2t,
∴∠PBQ=∠PQB=
=30°,
∵∠BHQ=90°,
∴PH=t,QH=
t,
延长HQ交y轴于点S,
∵∠HAO=∠AHS=∠AOS=90°,
∴四边形AHSO是矩形,
∴QK=OS=AH=4-BH=4-3t,OK=OA-AK=4
-HQ=4
-
t
∴Q(4
-
t,4-3t)
代入抛物线解析式4-3t=
(4
-
t)2-
(4
-
t)+4;
解得t1=1,t2=0(舍去),

(3)如图2,在△ABE中,
∵∠BAE=90°,∠ABE=30°,
∴tan∠ABE=tan30°=
,
∴
=
,
∴AE=
,
∵OE=OA-AE,
∴OE=
,
∴E(
,0),
取OE的中点M,连接MG、CM,
则MG=
OE=
,CM=
,
∵CG+GM≥CM,
∴当G在CM上时AE,CG最短
作GN⊥y轴,GR⊥x轴,
=
=
,
设GN=
k,
则CN=3k,RG=ON=4-3k,
∴G(
k,4-3k),MR=
-
k,
由勾股定理得,MR2+RG2=MG2,
即(
-
k)2+(4-3k)2=(
)2,
解得k1=
,k2=2(舍去)
G(
,2),m=
,G点不在抛物线上.
 解:(1)如图1,在四边形ABCO中,
解:(1)如图1,在四边形ABCO中,∵BA⊥x轴,
∴∠BAO=90°,
∵BC∥x轴,
∴∠ABC=∠BAO=90°,
∴四边形ABCD是矩形,
∴AB=OC=4,BC=OA=4
| 3 |
∴点C的坐标为(0,4),
依题意可得:
|
解得
|
∴所求抛物线的解析式为y=
| 1 |
| 3 |
4
| ||
| 3 |
(2)如图1,过Q作x轴垂线,垂足为K,QH⊥AB,垂足为H.
在RT△ABO中,tan∠ABO=
| OA |
| AB |
| 3 |
∴∠ABO=60°,
∵PQ∥OB,
∴∠QPA=∠ABO=60°
∴∠QPB=180°-60°=120°,
∵PB=PQ=2t,
∴∠PBQ=∠PQB=
| 180°-120° |
| 2 |
∵∠BHQ=90°,
∴PH=t,QH=
| 3 |
延长HQ交y轴于点S,
∵∠HAO=∠AHS=∠AOS=90°,
∴四边形AHSO是矩形,
∴QK=OS=AH=4-BH=4-3t,OK=OA-AK=4
| 3 |
| 3 |
| 3 |
∴Q(4
| 3 |
| 3 |
代入抛物线解析式4-3t=
| 1 |
| 3 |
| 3 |
| 3 |
4
| ||
| 3 |
| 3 |
| 3 |
解得t1=1,t2=0(舍去),

(3)如图2,在△ABE中,
∵∠BAE=90°,∠ABE=30°,
∴tan∠ABE=tan30°=
| AE |
| AB |
∴
| AE |
| 4 |
| ||
| 3 |
∴AE=
4
| ||
| 3 |
∵OE=OA-AE,
∴OE=
8
| ||
| 3 |
∴E(
8
| ||
| 3 |
取OE的中点M,连接MG、CM,
则MG=
| 1 |
| 2 |
4
| ||
| 3 |
8
| ||
| 3 |
∵CG+GM≥CM,
∴当G在CM上时AE,CG最短
作GN⊥y轴,GR⊥x轴,
| OM |
| OC |
| NG |
| CN |
| ||
| 3 |
设GN=
| 3 |
则CN=3k,RG=ON=4-3k,
∴G(
| 3 |
4
| ||
| 3 |
| 3 |
由勾股定理得,MR2+RG2=MG2,
即(
4
| ||
| 3 |
| 3 |
4
| ||
| 3 |
解得k1=
| 2 |
| 3 |
G(
2
| ||
| 3 |
| 8 |
| 3 |
点评:本题考查了待定系数法求解析式,根据三角函数解直角三角形,等腰三角形的性质以及平行线分线段定理,勾股定理的应用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若点P在第二象限,点P到x轴的距离是4,到y轴的距离是3,点P的坐标是( )
| A、(-4,3) |
| B、(4,-3) |
| C、(-3,4) |
| D、(3,-4) |
 如图,点P是OO的直径BA延长线上一点,PC与OO相切于点C,CD⊥AB,垂足为H,连接AC、AD、OC、BC,则下列结论中不一定正确的是( )
如图,点P是OO的直径BA延长线上一点,PC与OO相切于点C,CD⊥AB,垂足为H,连接AC、AD、OC、BC,则下列结论中不一定正确的是( )| A、OC⊥PC |
| B、AC=AD |
| C、AD∥OC |
| D、∠PCA=∠OCB |
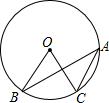 如图,在⊙O中,∠BOC=60°,则∠BAC等于( )
如图,在⊙O中,∠BOC=60°,则∠BAC等于( )| A、60° | B、50° |
| C、40° | D、30° |
 如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果
如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果
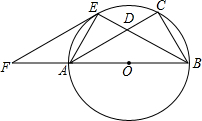 如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.