题目内容
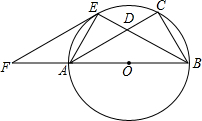 如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.(1)求证:EF是⊙O切线;
(2)若EF=10,tan∠AEF=
| 1 |
| 2 |
考点:切线的判定
专题:
分析:(1)要证EF是⊙O的切线,只要连接OE,再证∠FEO=90°即可;
(2)连接CE,可证明△FEA∽△ECD,得出
=
,即AE•EC=CD•EF,再由AE=CE,即可得出AE2=CD•EF,然后证明△FEA∽△FBA,得出AE,BF的比例关系式,根据勾股定理得出AE,BF的关系式,求出AE的长,即可得出CD的长.
(2)连接CE,可证明△FEA∽△ECD,得出
| EF |
| EC |
| EA |
| CD |
解答: (1)证明:连接OE,
(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴OE⊥EF,
∴EF是⊙O切线.
(2)解:连接CE,
∵∠FEA=∠OEB,∠OBE=∠OEB,
∴∠FEA=∠EBA,
∴△AEF∽△EBF,
∴
=
,
∵tan∠AEF=
,EF=10,
∴tan∠EBF=
=
,
∴FB=20,
∵EF2=AF•BF,
∴AF=
=5,
∴AB=BF-AF=15,
∵AE2+BE2=AB2,BE=2AE,
∴AE=3
,
∵∠B的平分线BE交AC于D,
∴AE=CE,
∵EF∥AC,
∴∠F=∠BAC,
∵∠FEA=∠OEB,∠OBE=∠ACE,
∴∠FEA=∠ECA,
∴△FEA∽△ECD,
∴
=
,
即AE•EC=CD•EF,
∴AE2=CD•EF;
∴DC=
=4.5.
 (1)证明:连接OE,
(1)证明:连接OE,∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴OE⊥EF,
∴EF是⊙O切线.
(2)解:连接CE,
∵∠FEA=∠OEB,∠OBE=∠OEB,
∴∠FEA=∠EBA,
∴△AEF∽△EBF,
∴
| FB |
| EF |
| EB |
| AE |
∵tan∠AEF=
| 1 |
| 2 |
∴tan∠EBF=
| EB |
| AE |
| 1 |
| 2 |
∴FB=20,
∵EF2=AF•BF,
∴AF=
| EF2 |
| BF |
∴AB=BF-AF=15,
∵AE2+BE2=AB2,BE=2AE,
∴AE=3
| 5 |
∵∠B的平分线BE交AC于D,
∴AE=CE,
∵EF∥AC,
∴∠F=∠BAC,
∵∠FEA=∠OEB,∠OBE=∠ACE,
∴∠FEA=∠ECA,
∴△FEA∽△ECD,
∴
| EF |
| EC |
| EA |
| CD |
即AE•EC=CD•EF,
∴AE2=CD•EF;
∴DC=
| AE2 |
| EF |
点评:本题考查了切线的判定以及相似三角形的判定和性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
?ABCD的周长为36cm,AB=2BC,则较长边的长为( )
| A、15cm | B、6cm |
| C、12cm | D、10.5cm |
 如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置. (1)请你任意写5个正的真分数:
(1)请你任意写5个正的真分数: