Question

2．△ABC的边BC=$\frac{1}{2}$（AB+AC），取AB，AC中点M，N，G为重心，I为内心．试证：过A，M，N三点的圆与直线GI相切．

Answer 1

分析 先由三角形内角平分线定理结合等比性质得到$\frac{AI}{IE}$=2，再由△ABE∽△FCE得到比例，结合比例的性质即可．

解答 解：如图，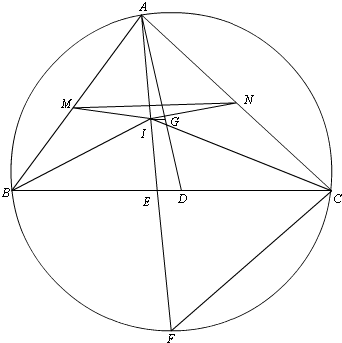

延长AG交BC于D；延长AI分别交BC、△ABC的外接圆于E、F．
∵I是△ABC的内心，
∴∠ABI=∠IBE、∠ACI=∠ICE，
∴由三角形内角平分线定理，有：$\frac{AI}{IE}=\frac{AB}{BE}$，$\frac{AI}{IE}=\frac{AC}{CE}$，
∴由等比定理，得：$\frac{AI}{IE}$=$\frac{AB+AC}{BE+CE}$=$\frac{AB+BC}{BC}$，
∵BC=$\frac{AB+AC}{2}$，
∴$\frac{AI}{IE}$=2．
∵M、N分别是AB、AC的中点，
∴G是△ABC的重心，
∴$\frac{AG}{GD}$=2=$\frac{AI}{IE}$，
∴GI∥BC．
∵M、N分别是AB、AC的中点，
∴MN∥BC，
∴GI∥MN．
∵I是△ABC的内心，
∴∠BAE=∠CAE．
∵A、B、F、C共圆，
∴∠BCF=∠BAE，
∴∠BAE=∠CAE，
∴∠BCF=∠CAE．
由三角形外角定理，有：∠FIC=∠CAE+∠ACI，
∵∠BCF=∠CAE，∠ACI=∠BCI，
∴∠FIC=∠BCF+∠BCI=∠FCI，
∴FC=FI．
∵A、B、F、C共圆，
∴△ABE∽△FCE，
∴$\frac{AB}{FC}=\frac{BE}{FE}$，
∴$\frac{AB}{BE}=\frac{FC}{FE}$，
∵$\frac{AI}{IE}=\frac{AB}{BE}$，
∴$\frac{FC}{FE}=\frac{AI}{IE}$，
∵FC=FI，$\frac{AI}{IE}$=2，
∴$\frac{FI}{FE}$=2，
∴$\frac{FI}{EF-FI}=\frac{2}{1-2}$，
∴$\frac{FI}{IE}$=2，
∴AI=FI，
∵AN=CN，
∴IN∥FC，
∴∠AIN=∠AFC．
∵A、B、F、C共圆，
∴∠AFC=∠ABC，
∴∠AIN=∠ABC．
∵MN∥BC，
∴∠AMN=∠ABC，
∴∠AIN=∠AMN，
∴A、M、I、N共圆，
∴∠NMI=∠NAI．
∵∠MAI=∠NAI、∠NMI=∠NAI，
∴∠NMI=∠MAI．
∵MN∥GI，
∴∠MIG=∠NMI，
∵∠NMI=∠MAI，
∴∠MIG=∠MAI，
∴GI是△AMN的外接圆的切线．

点评 此题三角形五心综合题，主要考查了四点共圆的性质和判定，相似三角形的判定和性质，比例的性质，三角形内角和外角定理，解本题的关键是四点共圆的应用和判定，难点是比例的推导．