题目内容
14. 实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a-b|-|a|的结果为( )| A. | -2a+b | B. | -b | C. | -2a-b | D. | b |
分析 根据绝对值的意义,可化简绝对值,根据整式的运算,可得答案.
解答 解:由题意,得
原式=b-a-(-a)
=b-a+a
=b,
故选:D.
点评 本题考查了实数与数轴,利用绝对值的意义化简绝对值是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.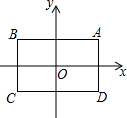 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
19.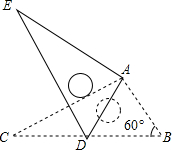 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ABD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
 (1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
(1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号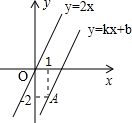 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象互相平行,且经过点A,则一次函数y=kx+b的解析式为y=2x-4.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象互相平行,且经过点A,则一次函数y=kx+b的解析式为y=2x-4.
 如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.