题目内容
7.根据不等式基本性质,把下列各式化成“x>a”或“x<a”的形式(1)3x>2;
(2)2x+3<0;
(3)x-3<3x-2;
(4)-2x+1<x+3.
分析 (1)根据不等式的性质2,两边同除以3,可以解答本题;
(2)根据不等式的性质1和2可以解答本题;
(3)根据不等式的性质1和不等式的性质3可以解答本题;
(4)根据不等式的性质1和不等式的性质3可以解答本题.
解答 解:(1)3x>2
不等式两边同时除以3,得
3x÷3>2÷3
解得,x>$\frac{2}{3}$;
(2)2x+3<0
两边同时减去3,得
2x<-3
两边同时除以2,得
x<$-\frac{3}{2}$;
(3)x-3<3x-2
两边同时加3,得
x<3x+1,
两边同时减去3x,得
-2x<1,
两边同时除以-2,得
x>-$\frac{1}{2}$;
(4)-2x+1<x+3
两边同时减去1,得
-2x<x+2
两边同时减去x,得
-3x<2
两边同时除以-3,得
x>$-\frac{2}{3}$.
点评 本题考查不等式的性质,解题的关键是明确不等式的性质,尤其是要注意不等式的性质3,不等式两边同时乘以或除以同一个负数,不等式的符号要改变.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
19.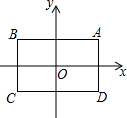 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,且A′B′=2AB.已知mn=3(m,n为正实数),在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则t的值等于( )| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
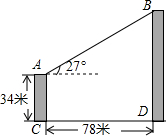 如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米)
如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米) (1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
(1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号 如图是一个物体的三视图,根据图中尺寸(单位:cm),它的体积为32+8πcm3.
如图是一个物体的三视图,根据图中尺寸(单位:cm),它的体积为32+8πcm3. 如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.