题目内容
11．在△ABC中，AB=AC，AB边的中垂线交AC于D，交AB于E（1）请画出图形，指出图中所有相等的线段，并说明理由；
（2）若△ABC的周长为16，△BCD的周长为10，求△ABC的三边长．
分析 （1）根据线段的垂直平分线的定义和尺规作图画图即可；
（2）根据线段的垂直平分线的性质和三角形的周长公式计算即可．
解答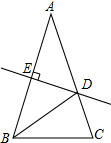 
解：（1）∵DE是AB边的中垂线，
∴DA=DB，AE=BE；
（2）△BCD的周长=BC+CD+DB=BC+AC=10，
△ABC的周长=BC+AC+AB=16，
∴AB=6，
则AC=AB=6，BC=4．
点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19．
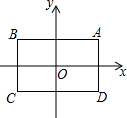如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）
如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）| A． | $\frac{3}{4}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | $\frac{3}{2}$ |
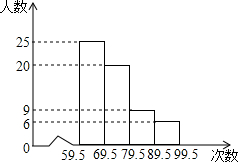如图是九年级（1）班同学的一次体检每分钟心跳次数的频数分布直方图（次数均为整数）．已知该班只有5位同学的心跳每分钟75次．请观察图回答：
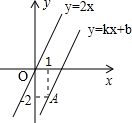如图，一次函数y=kx+b的图象与正比例函数y=2x的图象互相平行，且经过点A，则一次函数y=kx+b的解析式为y=2x-4．