题目内容
1.用配方法解下列方程(1)3x2-27=0
(2)(x+6)2-9=0
(3)x2-2x-5=0
(4)x2+x-1=0.
分析 (1)(2)直接移项开方即可;
(3)(4)把左边配成完全平方式,右边化为常数,然后运用直接开方法解方程即可.
解答 解:(1)3x2-27=0
3x2=27
x2=9
x1=3,x2=-3;
(2)(x+6)2-9=0
(x+6)2=9
x+6=±3
x1=-3,x2=-9;
(3)x2-2x-5=0
移项配方得x2-2x+1=6,
即(x-1)2=6,
解得x-1=±$\sqrt{6}$,
则x1=1+$\sqrt{6}$,x2=1-$\sqrt{6}$;
(4)x2+x-1=0,
移项配方得x2+x+$\frac{1}{4}$=$\frac{5}{4}$,
即(x+$\frac{1}{2}$)2=$\frac{5}{4}$,
解得x+$\frac{1}{2}$=±$\frac{\sqrt{5}}{2}$,
则x1=$\frac{\sqrt{5}-1}{2}$,x2=$\frac{-\sqrt{5}-1}{2}$.
点评 本题考查的是用配方法解一元二次方程的步骤:形如x2+px+q=0型:第一步移项,把常数项移到右边;第二步配方,左右两边加上一次项系数一半的平方;第三步左边写成完全平方式;第四步,直接开方即可.

练习册系列答案
相关题目
12.从标有号数1~100的100张卡片中随意抽取1张,其号数为2或3的倍数的概率( )
| A. | $\frac{33}{100}$ | B. | $\frac{4}{25}$ | C. | $\frac{67}{100}$ | D. | $\frac{1}{2}$ |
10.下列各组中的两个二次根式,是同类二次根式的是( )
| A. | $\sqrt{0.36}$与$\sqrt{3.6}$ | B. | $\sqrt{xy}$与$\sqrt{x+y}$ | C. | $\sqrt{5{x}^{2}y}$与$\sqrt{5x{y}^{2}}$ | D. | $\sqrt{x-y}$与$\sqrt{\frac{{x}^{2}-{y}^{2}}{x+y}}$ |
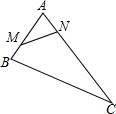 如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?
如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似? 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.