题目内容
12.从标有号数1~100的100张卡片中随意抽取1张,其号数为2或3的倍数的概率( )| A. | $\frac{33}{100}$ | B. | $\frac{4}{25}$ | C. | $\frac{67}{100}$ | D. | $\frac{1}{2}$ |
分析 根据题意分别得出号数是2的倍数以及是3的倍数的个数,进而利用概率公式求出即可.
解答 解:∵从标有号数1~100的100张卡片中随意抽取1张,
∴号数为2的倍数的有:2,3,4,6,8,10..100共50个,
号数为3的倍数的有:3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,48,51,
54,57,60,63,66,69,72,75,78,81,84,87,90,93,96,99,共33个,
其中偶数16个重复,故符合题意号数为2或3的倍数的概率为:$\frac{50+17}{100}$=$\frac{67}{100}$.
故选:C.
点评 此题主要考查了概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.若规定:1!!=1,2!!=-2×1,3!!=3×2×1,4!!=-4×3×2×1,则$\frac{2016!!}{2015!!}$的值为( )
| A. | -2016 | B. | 2016 | C. | 2015 | D. | -2015 |
 如图,已知∠A=∠B=90°,∠BCD,∠ADC的平分线交AB于E.求证:
如图,已知∠A=∠B=90°,∠BCD,∠ADC的平分线交AB于E.求证: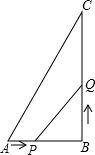 如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P,Q以1cm/s的速度分别从A,B出发,点P从A到B,点Q从B到C.
如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,点P,Q以1cm/s的速度分别从A,B出发,点P从A到B,点Q从B到C.