题目内容
3.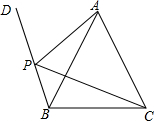 如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.
如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.(1)求证:∠APC=∠APD;
(2)若∠BAC=60°,BP=3,PA=4,求PC的长.
分析 (1)根据等腰三角形的性质得到∠ABC=∠ACB,根据A、P、B、C四点共圆得到∠APC=∠ABC,等量代换即可得到答案;
(2)在射线BP上截取PH=PA,证明△HAB≌△PAC,根据全等三角形的性质得到答案.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠BPC=∠BAC,
∴A、P、B、C四点共圆,
∴∠APC=∠ABC,
∴∠APC=∠ACB,又∠APD=∠ACB,
∴∠APC=∠APD;
(2)解:在射线BP上截取PH=PA,
∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∴∠APH=60°,又PH=PA,
∴△APH是等边三角形,
∴∠HAP=60°,AH=AP,
在△HAB和△PAC中,
$\left\{\begin{array}{l}{AH=AP}\\{∠HAB=∠PAC}\\{AB=AC}\end{array}\right.$,
∴△HAB≌△PAC,
∴PC=BH=BP+PH=BP+PA=7.
点评 本题考查的是全等三角形的判定和性质、等边三角形的性质,掌握全等三角形的判定定理和性质定理、等边三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
16.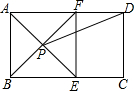 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.(1)求证:四边形ABEF是正方形;
(2)如果AB=4,AD=7,求tan∠ADP的值.
3.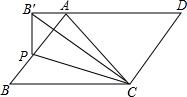 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
 如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP长度为( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
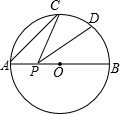 如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$.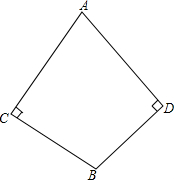 如图,四边形ACBD中,∠C=∠D=90°,BC=BD.求证:AC=AD.
如图,四边形ACBD中,∠C=∠D=90°,BC=BD.求证:AC=AD.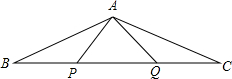 如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.
如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.