题目内容
13.在等腰Rt△ABC中,AC=BC=4cm,D点为BC边中点,E为斜边AB上任意一点,则CE+DE的最小值为2$\sqrt{5}$.分析 首先确定动点E何位置时,DE+BE的值最小.即DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.
解答 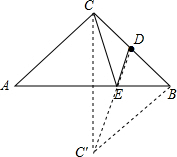 解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,
解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,
此时DC′=DE+EC′=DE+CE的值最小.
连接CB′,易证CB′⊥BC,
根据勾股定理可得DC′=2$\sqrt{5}$cm.
故CE+DE的最小值为2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 此题考查了线路最短的问题,确定动点E何位置时,使DE+BE的值最小是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.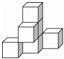 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )
 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )| A. | 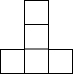 | B. | 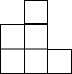 | C. | 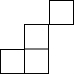 | D. | 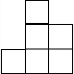 |
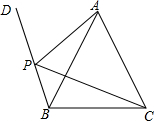 如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.
如图,在△ABC中,AB=AC,射线BD上有一点P,且∠BPC=∠BAC.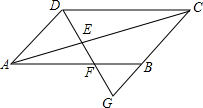 如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.
如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.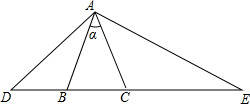 如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数.
如图,△ABC中,AB=AC,∠BAC=α,D,E分别在底边CB,BC的延长线上,当AB2=DB•CE时,求∠DAE的度数.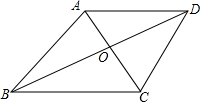 菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$
菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$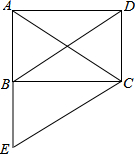 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥BD,交AB的延长线于点E.
如图,四边形ABCD是矩形,对角线AC、BD相交于点O,CE∥BD,交AB的延长线于点E.