题目内容
20.已知关于x的一元二次方程ax2-(a+2)x+2=0有两个不相等的正整数根时,整数a的值是a=1.分析 由一元二次方程的定义可得出a≠0,再利用根的判别式△=b2-4ac,套入数据即可得出△=(a-2)2≥0,可得出a≠2且a≠0,设方程的两个根分别为x1、x2,利用根与系数的关系可得出x1•x2=$\frac{2}{a}$,再根据x1、x2均为正整数,a为整数,即可得出结论.
解答 解:∵方程ax2-(a+2)x+2=0是关于x的一元二次方程,
∴a≠0.
∵△=(a+2)2-4a×2=(a-2)2≥0,
∴当a=2时,方程有两个相等的实数根,
当a≠2且a≠0时,方程有两个不相等的实数根.
∵方程有两个不相等的正整数根,
∴a≠2且a≠0.
设方程的两个根分别为x1、x2,
∴x1•x2=$\frac{2}{a}$,
∵x1、x2均为正整数,
∴$\frac{2}{a}$为正整数,
∵a为整数,a≠2且a≠0,
∴a=1,
故答案为:a=1.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是:①找出△=(a-2)2≥0;②找出x1•x2=$\frac{2}{a}$为正整数.本题属于中档题,难度不大,解决该题型题目时,由方程的两根均为整数确定a的值是难点.

练习册系列答案
相关题目
15. 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )| A. | $\frac{3\sqrt{15}}{2}$ | B. | 8 | C. | 2$\sqrt{15}$ | D. | 9 |
 如图,在等边△ABC中,边长为30,点M为线段AB上一动点,将等边△ABC沿过M的直线折叠,折痕与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,设折痕为MN,则AN的值为21或65.
如图,在等边△ABC中,边长为30,点M为线段AB上一动点,将等边△ABC沿过M的直线折叠,折痕与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,设折痕为MN,则AN的值为21或65. 如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20.
如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20.
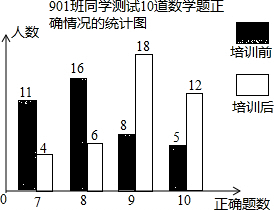 小潘老师为了检测901班同学培训效果做了一项教学实验:通过测试10道数学题了解培训前和培训后学生的解题情况.并绘成如下的条形统计图.根据统计图,回答下列问题:
小潘老师为了检测901班同学培训效果做了一项教学实验:通过测试10道数学题了解培训前和培训后学生的解题情况.并绘成如下的条形统计图.根据统计图,回答下列问题: 如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.
如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.