题目内容
7.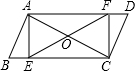 如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.
如图,已知?ABCD中,E,F分别在边BC,AD上,且BE=DF,AC,EF相交于O,连接AE,CF.(1)求证:AE=CF;
(2)若∠FOC=2∠OCE,求证:四边形AECF是矩形.
分析 (1)只要证明四边形AECF是平行四边形即可解决问题;
(2)只要证明AC=EF即可解决问题.
解答 证明:(1) ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BD,
∵BE=DF,
∴AF=CE,AF∥EC,
∴四边形AECF是平行四边形,
∴AE=CF.
(2)∵∠FOC=∠OEC+∠OCE=2∠OCE,
∴∠OEC=∠OCE,
∴OE=OC,
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∴AC=EF,
∴四边形AECF是矩形.
点评 本题考查平行四边形的性质、矩形的判定和性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.

练习册系列答案
相关题目
15. 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
 如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )
如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2$\sqrt{15}$,则线段CE的长为( )| A. | $\frac{3\sqrt{15}}{2}$ | B. | 8 | C. | 2$\sqrt{15}$ | D. | 9 |
3. 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )
 如图所示,下列说法正确的是( )
如图所示,下列说法正确的是( )| A. | 如果∠1=∠4,那么AB∥CD | B. | 如果∠2=∠3,那么AE∥DF | ||
| C. | 如果∠1=∠3,那么AB∥DF | D. | 如果∠2=∠4,那么AE∥DC |
4.某新建火车站站前有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),则人行通道的宽度是( )


| A. | 1 米 | B. | 2米 | C. | $\frac{26}{3}$米 | D. | 2米或$\frac{26}{3}$米 |

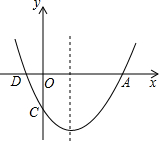 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,-3),对称轴是直线x=1. 如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.
如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$. 如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.
如图所示,图中是某中学初一(1)班某次期中考试成绩各个分数段人数的统计图,已知其中不及格同学的人数占全班人数的$\frac{1}{13}$.