题目内容
12.长春地铁正在紧张施工,现有大量沙石需要运输,某车队现有载重量为8吨的甲种卡车5辆,载重量为10吨的乙种卡车7辆,随着工程的进展,车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆(可以只增购一种),车队有多少种方案?分析 设购买甲种卡车x辆,则购买乙种卡车(6-x)辆.利用“车队需要一次运输沙石165吨以上”得出不等式求出购买方案即可.
解答 解:设购买甲种卡车x辆,则购买乙种卡车(6-x)辆.
依题意得:8(5+x)+10(7+6-x)>165,
解得x<2.5.
根据题意,x为非负整数,所以x=0,x=1,x=2.
所以车队有3种购买方案:
方案一:不购买甲种卡车,购买乙种卡车6辆;
方案二:购买甲种卡车1辆,购买乙种卡车5辆;
方案三:甲种卡车2辆,购买乙种卡车4辆.
点评 此题主要考查了二元一次不等式的应用,根据已知得出正确的不等式关系是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6cm,则AB的长是( )| A. | 3cm | B. | 6cm | C. | 10cm | D. | 12cm |
20.观察下表:
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为16x+9y,第4格的“特征多项式”为25x+16y,第n格的“特征多项式”为(n+1)2x+n2y;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x y y y x x x x | … |
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16.
①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由.
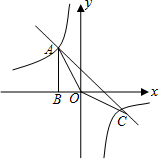 如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$
如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$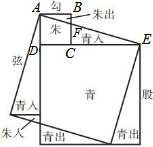 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.