题目内容
7. 如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.
如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.
分析 首先证明△BPC∽△MBC,得到$\frac{CP}{BC}=\frac{PB}{BM}=\frac{BC}{MC}$,进而证明CP/CD=BP/BN;由∠PCD=∠BMC=∠PBC,证明△BPN∽△PDC,得到∠BPN=∠CPD,即可解决问题.
解答  解:如图,∵四边形ABCD为正方形,
解:如图,∵四边形ABCD为正方形,
∴BC=CD,AB∥CD,∠ABC=∠BCD,
∴∠PCD=∠BMC,
∵BP⊥MC,
∴∠PBC+∠BCM=90°,而∠PBC+∠PBM=90°,
∴∠PBC=∠BMC,∠MCB=∠BCP,
∴△BPC∽△MBC;
∴CP:BC=BP:BM=BC:MC,
∵BM=BN,BC=CD,
∴CP:CD=BP:BQ,而∠PCD=∠BMC=∠PBC,
∴△BPN∽△PDC,
∴∠BPN=∠CPD,∠CPD+∠NPC=90°,
∴DP⊥PN.
点评 本题考查正方形的性质、相似三角形的判定及其性质等几何知识点应用为核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
12.某市出租车收费标准如下表所示,根据此收费标准,解决下列问题:.
(1)若行驶路程为5km,则打车费用为11.2元;
(2)若行驶路程为x(km)(x>6),则打车费用为(2.4x-1.6)元;(用含x的代数式表示)
(3)当打车费用为27.2元时,行驶路程为多少千米?
| 行驶里程 | 收费标准 |
| 不超出3km的部分 | 起步价7元,燃油附加费1元 |
| 超出3km不超出6km的部分 | 1.6元/km |
| 超出6km的部分 | 2.4元/km |
(2)若行驶路程为x(km)(x>6),则打车费用为(2.4x-1.6)元;(用含x的代数式表示)
(3)当打车费用为27.2元时,行驶路程为多少千米?
17.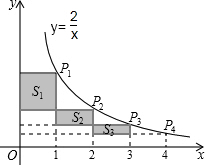 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
 如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )
如图,在反比例函数y=$\frac{2}{x}$(x>0)的图象上,有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,则S1+S2+S3=( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
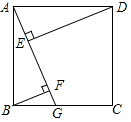 如图,G是正方形ABCD边BC上一动点(不与B、C重合).DE⊥AG于E,BF⊥AG于F,试探究线段DE、EF、BF之间满足怎样的数量关系,写出你的结论,并写出证明过程.
如图,G是正方形ABCD边BC上一动点(不与B、C重合).DE⊥AG于E,BF⊥AG于F,试探究线段DE、EF、BF之间满足怎样的数量关系,写出你的结论,并写出证明过程.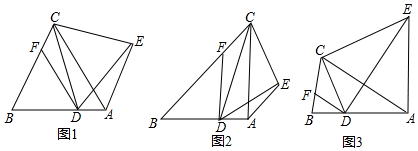
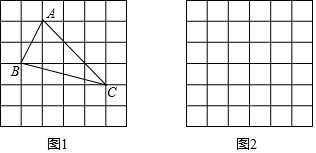
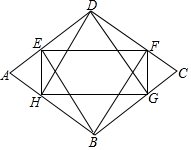 如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.
如图,在菱形ABCD中,分别过B、D作对边的垂线,垂足分别为E、F、G、H.若四边形EFGH的面积与菱形ABCD的面积之比为4:9,则sinA=$\frac{2\sqrt{2}}{3}$或$\frac{\sqrt{5}}{3}$.