题目内容
已知Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，CD、C′D′分别是两个三角形斜边上的高，且
=
，求证：△ABC∽△A′B′C′．
| CD |
| C′D′ |
| AC |
| A′C′ |
考点：相似三角形的判定
专题：证明题
分析：先根据题意得出∠ADC=∠A′D′C′=90°，再由
=
得出△ADC∽△A'D'C'，故可得出∠A=∠A′，再由∠C=∠C’=90°即可得出结论．
| CD |
| C′D′ |
| AC |
| A′C′ |
解答：证明：∵CD、C′D′分别是两个三角形斜边上的高，
∴∠ADC=∠A′D′C′=90°，
∵
=
，
∴△ADC∽△A'D'C'，
∴∠A=∠A′，
∵∠C=∠C’=90°，
∴△ABC∽△A'B'C'．
∴∠ADC=∠A′D′C′=90°，
∵
| CD |
| C′D′ |
| AC |
| A′C′ |
∴△ADC∽△A'D'C'，
∴∠A=∠A′，
∵∠C=∠C’=90°，
∴△ABC∽△A'B'C'．
点评：本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．
练习册系列答案
相关题目
已知：⊙O和⊙O′交于A、B两点，过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点，GC、GD分别交⊙O和⊙O′于点E、F，求证：∠EAF=∠C+∠D．已知△ABC的内切圆⊙O切三角形的三边于点D，E，F，则△DEF是（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、都有可能 |
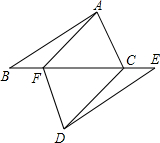如图，已知△ABF≌△DEC，且AC=DF，说明△ABC≌△DEF的理由．
如图，两个同心圆的半径分别为2cm和4cm，有大圆上一点A作小圆的两条切线AB、AC，切点为B、C，求图中阴影部分的面积．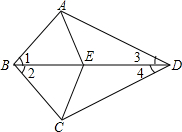
已知：如图，∠1=∠2，∠3=∠4，点E在BD上，连结AE、CE，求证：AE=CE．