题目内容
 如图,在△ABC中,D为BC的中点,DE⊥DF交AB、AC于E、F,求证:BE+CF>EF.
如图,在△ABC中,D为BC的中点,DE⊥DF交AB、AC于E、F,求证:BE+CF>EF.考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:延长ED,使DG=DE,连接CG、FG,可证△BDE≌△CDG,可得BE=CG、EF=FG,即可证明BE+CF>EF.
解答:解:延长ED,使DG=DE,连接CG、FG,

∵D为BC的中点,
∴BD=CD,
在△BDE和△CDG中,
,
∴△BDE≌△CDG(SAS),
∴BE=CG,EF=FG,
∵CG+CF>FG,
∴BE+CF>EF.

∵D为BC的中点,
∴BD=CD,
在△BDE和△CDG中,
|
∴△BDE≌△CDG(SAS),
∴BE=CG,EF=FG,
∵CG+CF>FG,
∴BE+CF>EF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中证明△BDE≌△CDG是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 已知:⊙O和⊙O′交于A、B两点,过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点,GC、GD分别交⊙O和⊙O′于点E、F,求证:∠EAF=∠C+∠D.
已知:⊙O和⊙O′交于A、B两点,过点B的直线分别交⊙O和⊙O′于点C、D、G是两圆外一点,GC、GD分别交⊙O和⊙O′于点E、F,求证:∠EAF=∠C+∠D.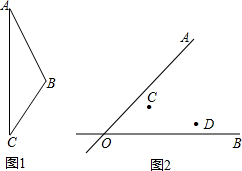 作图题:
作图题: 如图,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠BOC的度数为
如图,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠BOC的度数为