题目内容
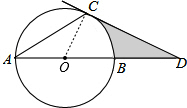
 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OC,结合切线的性质和条件可求得∠A=∠D=30°,可证明AC=CD;
(2)由(1)结合条件直角三角形的性质可求得CD,可求得△OCD和扇形OCB的面积,可求出阴影部分的面积.
(2)由(1)结合条件直角三角形的性质可求得CD,可求得△OCD和扇形OCB的面积,可求出阴影部分的面积.
解答:
(1)证明:如图,连接CO,
∵CD切⊙O于C,
∴∠OCD=90°,
∴∠OCA=∠OAC=30°,∠ADC=30°,
∴∠A=∠D,
∴AC=CD;
(2)解:由(1)知∠OCD=90°,∠ADC=30°,∠COD=60°,
∴OD=2OC=4,CD=2
,
∴S△OCD=
CD•OC=2
,S扇形OCB=
=
,
∴S阴影=2
-
.

∵CD切⊙O于C,
∴∠OCD=90°,
∴∠OCA=∠OAC=30°,∠ADC=30°,
∴∠A=∠D,
∴AC=CD;
(2)解:由(1)知∠OCD=90°,∠ADC=30°,∠COD=60°,
∴OD=2OC=4,CD=2
| 3 |
∴S△OCD=
| 1 |
| 2 |
| 3 |
| 60πOC2 |
| 360 |
| 2π |
| 3 |
∴S阴影=2
| 3 |
| 2π |
| 3 |
点评:本题主要考查切线的性质及扇形面积的计算,掌握过切点的半径与切线垂直是解题的关键.在(1)中注意OA=OC的运用,在(2)中先求得CD是解题的关键.

练习册系列答案
相关题目
某中学书法兴趣小组12名成员的年龄情况如下:
则这个小组成员年龄的众数和中位数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
| A、13,14 |
| B、13,15 |
| C、14,14 |
| D、15,16 |
下列结论错误的是( )
| A、sin60°-sin30°=sin30° | ||
| B、sin30°=cos60° | ||
C、tan60°=
| ||
| D、sin245°+cos245°=1 |
 如图,AB∥CD,∠B=50°,∠D=70°,则∠E=( )
如图,AB∥CD,∠B=50°,∠D=70°,则∠E=( )| A、40° | B、30° |
| C、20° | D、15° |
下列运算中错误的有( )
①
=-3,②
=-5,③±
=3,④
=4.
①
| -32 |
| (-5)2 |
| 32 |
| 16 |
| A、4 | B、3 | C、2 | D、1 |
 如图,∠3=∠4,试说明:∠1+∠2=180°.
如图,∠3=∠4,试说明:∠1+∠2=180°. 如图,AB∥CD,直线EF与AB、CD相交于点E、F,若∠1=60°,则∠2的度数是
如图,AB∥CD,直线EF与AB、CD相交于点E、F,若∠1=60°,则∠2的度数是 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.