题目内容
 (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.(2)如图:
 |
| AC |
 |
| CB |
考点:点与圆的位置关系,圆心角、弧、弦的关系
专题:
分析:(1)先由直径为10cm,可求半径为5cm,PA取得最大值是当点P在线段OA的延长线上时,由OA=12cm,可得PA的最大值为12+5=17cm,PA取得最小值是当点P在线段OA上时,可得PA的最小值为12-5=7cm;
(2)连接CO,由D、E分别是半径OA和OB的中点,可得OD=OE,由
=
,可得∠COD=∠COE,然后根据SAS可证△COD≌△COE,然后根据全等三角形的对应边相等即可得到CD=CE.
(2)连接CO,由D、E分别是半径OA和OB的中点,可得OD=OE,由
 |
| AC |
 |
| CB |
解答:(1)解:∵⊙O的直径为10cm,
∴⊙O的半径为10÷2=5(cm),
当点P在线段OA的延长线上时,PA取得最大值,当点P在线段OA上时,PA取得最小值
∵OA=12cm,
∴PA的最大值为12+5=17cm,PA的最小值为12-5=7cm;
(2)证明:连接CO,如图所示,
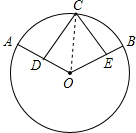
∵OA=OB,且D、E分别是半径OA和OB的中点,
∴OD=OE,
又∵
=
,
∴∠COD=∠COE,
在△COD和△COE中,
,
∴△COD≌△COE(SAS),
∴CD=CE.
∴⊙O的半径为10÷2=5(cm),
当点P在线段OA的延长线上时,PA取得最大值,当点P在线段OA上时,PA取得最小值
∵OA=12cm,
∴PA的最大值为12+5=17cm,PA的最小值为12-5=7cm;
(2)证明:连接CO,如图所示,

∵OA=OB,且D、E分别是半径OA和OB的中点,
∴OD=OE,
又∵
 |
| AC |
 |
| CB |
∴∠COD=∠COE,
在△COD和△COE中,
|
∴△COD≌△COE(SAS),
∴CD=CE.
点评:此题考查了点与圆的位置关系及圆周角定理,(1)的解题关键是:弄清PA取得最大值是当点P在线段OA的延长线上时;PA取得最小值是当点P在线段OA上时.

练习册系列答案
相关题目
下列运算中错误的有( )
①
=-3,②
=-5,③±
=3,④
=4.
①
| -32 |
| (-5)2 |
| 32 |
| 16 |
| A、4 | B、3 | C、2 | D、1 |
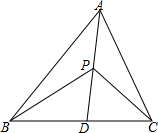 如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )
如图,△ABC中,AB>AC,AD是∠A的平分线,点P是线段AD上的任意一点,则AB+PC与AC+PB的大小关系是( )| A、AB+PC>AC+PB |
| B、AB+PC<AC+PB |
| C、AB+PC=AC+PB |
| D、不确定 |
 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.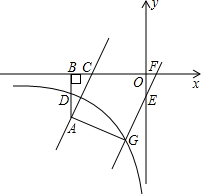 如图,点A在反比例函数y=
如图,点A在反比例函数y=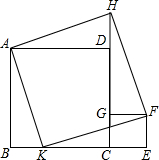 已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.