题目内容
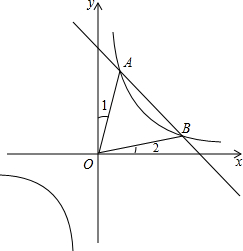 如图已知函数y1=
如图已知函数y1=| k1 |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:作AC⊥y轴于C,BD⊥x轴于D,根据题意求得B的坐标为(4,1),然后把A、B的坐标代入y2=k2x+b根据待定系数法即可求得解析式.
解答:
解:作AC⊥y轴于C,BD⊥x轴于D,
∵已知函数y1=
的图象经过A(1,4),
∴k1=4,
∴S△OAC=S△BOD=
×4=2,
∵∠OCA=∠ODB=90°,∠1=∠2,
∴△OAC∽△OBD,
=
=1,
∴B(4,1),
把A、B代入y2=k2x+b得
,
解得
,
∴y2表达式为y2=-x+5.
∵已知函数y1=
| k1 |
| x |
∴k1=4,
∴S△OAC=S△BOD=
| 1 |
| 2 |
∵∠OCA=∠ODB=90°,∠1=∠2,
∴△OAC∽△OBD,
| OC |
| OD |
| AC |
| BD |
∴B(4,1),
把A、B代入y2=k2x+b得
|
解得
|
∴y2表达式为y2=-x+5.
点评:本题考查了反比例函数图象与一次函数图象的交点问题以及系数k的几何意义,主要利用了待定系数法求函数解析.

练习册系列答案
相关题目
某中学书法兴趣小组12名成员的年龄情况如下:
则这个小组成员年龄的众数和中位数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
| A、13,14 |
| B、13,15 |
| C、14,14 |
| D、15,16 |
下列运算中错误的有( )
①
=-3,②
=-5,③±
=3,④
=4.
①
| -32 |
| (-5)2 |
| 32 |
| 16 |
| A、4 | B、3 | C、2 | D、1 |
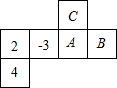 如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )
如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )| A、-2,-4,3 |
| B、3,-2,-4 |
| C、-2,3,-4 |
| D、3,-4,-2 |
 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.