题目内容
6.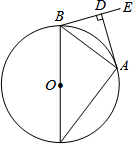 如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.
如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.(1)求证:AD为⊙O的切线;
(2)若tan∠ABD=$\frac{4}{3}$,AC=8,求⊙O的直径BC的长.
分析 (1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)根据三角函数的知识可求出AB,从而根据勾股定理求出BC的长,得出⊙O的直径.
解答 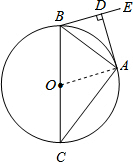 (1)略(2)10
(1)略(2)10
(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBE,AD⊥BE,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵∠DBA=∠CBA,tan∠ABD=$\frac{4}{3}$,AC=8,
∴tan∠CBA=$\frac{4}{3}$,
∴AB=$\frac{AC}{tan∠CBA}$=$\frac{8}{\frac{4}{3}}$=6,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴⊙O的直径BC为10.
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了三角函数的知识.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.某玩具厂广告称:“本厂工人工作时间为每天工作8小时,每月工作25天;待遇是熟练工人按时计件付工资,多劳多得,计件工资每月下来不少于900元,每月另加福利工资100元,按月结算…”该厂只生产两种玩具:小狗和小汽车,熟练工人晓云元月份领工资一千多元,她记录了如下表的一些数据:
(1)制作一个小狗和一辆小汽车各需要多少时间?
(2)制作一个小狗和一辆小汽车的计件工资各是多少元?
(3)假设晓云的工作效率不变,并且按时上下班,若晓云想二月份领工资不少于1115元,那么她二月份至少要生产小汽车多少个?
(4)元月份制作小狗和小汽车的数目没有限制,从二月份开始,厂方从销售方面考虑逐月调整为:k月份每个工人生产的小狗的个数不少于生产的小汽车的个数的k倍(k=2,3,4,…,12),假设晓云的工作效率不变,且服从工厂的安排,请运用所学数学知识说明厂家广告是否有欺诈行为?
| 小狗件数(单位:个) | 小汽车个数(单位:个) | 总时间(单位:分) | 总工资(单位:元) |
| 1 | 1 | 35 | 2.80 |
| 2 | 2 | 70 | 5.60 |
| 3 | 2 | 85 | 6.65 |
(2)制作一个小狗和一辆小汽车的计件工资各是多少元?
(3)假设晓云的工作效率不变,并且按时上下班,若晓云想二月份领工资不少于1115元,那么她二月份至少要生产小汽车多少个?
(4)元月份制作小狗和小汽车的数目没有限制,从二月份开始,厂方从销售方面考虑逐月调整为:k月份每个工人生产的小狗的个数不少于生产的小汽车的个数的k倍(k=2,3,4,…,12),假设晓云的工作效率不变,且服从工厂的安排,请运用所学数学知识说明厂家广告是否有欺诈行为?
14. 如图所示,∠1+∠2+∠3+∠4等于( )
如图所示,∠1+∠2+∠3+∠4等于( )
 如图所示,∠1+∠2+∠3+∠4等于( )
如图所示,∠1+∠2+∠3+∠4等于( )| A. | 180° | B. | 360° | C. | 240° | D. | 540° |
16. 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )
如图所示,已知直线a∥b,c与a,b均相交,∠1=60°,则∠2为( )| A. | 60° | B. | 70° | C. | 120° | D. | 150° |
 在下列四个三角形中,不能由△ABC经过旋转或平移得到的是( )
在下列四个三角形中,不能由△ABC经过旋转或平移得到的是( )



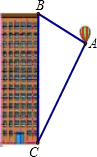 如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)? 已知a,b在数轴上的位置如图所示,化简:|b-a|+|a|=2a-b.
已知a,b在数轴上的位置如图所示,化简:|b-a|+|a|=2a-b.