题目内容
1.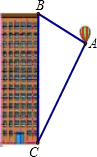 如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为35.6°,看这栋高楼底部的俯角的正切值为2,热气球与高楼的水平距离为90米,这栋高楼有多高(结果精确到0.1米.参考数据:sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
分析 首先由过点A作AD⊥BC于D,根据题意可得:∠BAD=35.6°,tan∠DAC=2,AD=90m,然后在Rt△ABD与Rt△ACD中,用正切函数计算即可求得答案.
解答 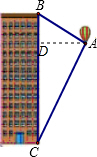 解:过点A作AD⊥BC于D,
解:过点A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
根据题意得:∠BAD=35.6°,tan∠DAC=2,AD=90m,
在Rt△ABD中,tan∠BAD=tan35.6°=$\frac{BD}{AD}$=$\frac{BD}{90}$≈0.716,
∴BD=64.44m,
在Rt△ACD中,tan∠CAD=$\frac{CD}{AD}=\frac{CD}{90}$=2,
∴CD=180m,
∴BC=BD+CD=64.44+180≈244.4(m).
∴这栋高楼有244.4m高.
点评 本题考查仰角与俯角的定义,要求学生能借助仰角,俯角构造直角三角形并解直角三角形.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
16.已知两圆的圆心距为5,两圆的半径分别是方程x2-6x+5=0的两根,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
13.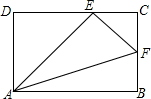 如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
 如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )| A. | △ABF∽△AEF | B. | △ABF∽△CEF | C. | △CEF∽△DAE | D. | △DAE∽△BAF |
11.如果关于x的一元二次方程(m+1)x2+x+m2-2m-3=0有一个根为0,则m的值( )
| A. | -1 | B. | 3 | C. | -1或3 | D. | 以上答案都不对 |
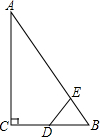 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,点D为BC的中点,动点E从点A出发,沿着A→B→A的方向以1cm/s的速度运动,当回到点A时停止运动,连接DE.设点E的运动时间为t(s),△BDE的面积为S(cm2)(这里规定:线段是面积为0的几何图形).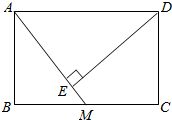 矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.
矩形ABCD中,M是BC的中点,DE⊥AM,E是垂足.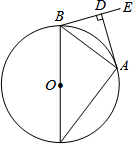 如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.
如图,已知:⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBE,AD⊥BE,垂足为D.