题目内容
6．在同一平面直角坐标系中，画出下列函数的图象：①y=3x+1；②y=-3x+1．观察图象，回答下列问题．（1）这两个函数的图象有什么共同特点？
（2）两条直线与y轴的交点坐标分别是什么？它们与函数表达式y=kx+b中的哪个量有关？
分析 利用画直线的方法画出两个函数的图象．（1）结合函数图象，即可寻找到两函数图象的共同特点；
（2）根据函数图象即可找出两条直线与y轴的交点坐标，令函数表达式y=kx+b中的x=0，即可求出函数y=kx+b与y轴的交点，再与y=kx+b进行比较即可得出结论．
解答 解：令x=0，y1=1，y2=1；
令y=0，则3x1+1=0和-3x2+1=0，解得：x1=-$\frac{1}{3}$，x2=$\frac{1}{3}$
故函数y=3x+1的图象过点（0，1）和（-$\frac{1}{3}$，0）；函数y=-3x+1的图象过点（0，1）（$\frac{1}{3}$，0）．
在坐标轴上画出两函数图象，如图所示．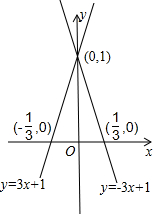
（1）观察两函数的图象发现：二者与x轴的夹角相同（锐角），均过相同的（0，1）点．
（2）两条直线与x轴的交点均为点（0，1），令y=kx+b中的x=0，则有y=b，
由此发现直线与y轴的交点坐标只与y=kx+b中的b值有关．
点评 本题考查了一次函数的图象，解题的关键是画出函数的图象．本题属于基础题，难度不大，解决该题型题目时，分别令x=0、y=0找出函数与坐标轴的交点坐标，根据交点坐标画出图象是关键．
练习册系列答案
阅读快车系列答案
相关题目
14．
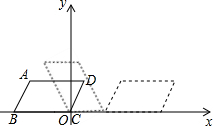已知，平行四边形ABCD在直角坐标系内的位置如图所示，且AB=2，BC=3，∠ABC=60°，点C在原点，把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转，经过505次翻转后，点A的坐标是（ ）
已知，平行四边形ABCD在直角坐标系内的位置如图所示，且AB=2，BC=3，∠ABC=60°，点C在原点，把平行四边形ABCD沿x轴正半轴作无滑动的连续翻转，经过505次翻转后，点A的坐标是（ ）| A． | （$\frac{2525}{2}$，$\sqrt{3}$） | B． | （$\frac{2521}{2}$，$\frac{3}{2}$$\sqrt{3}$） | C． | （1008，$\sqrt{3}$） | D． | （1008，$\frac{3}{2}$$\sqrt{3}$） |
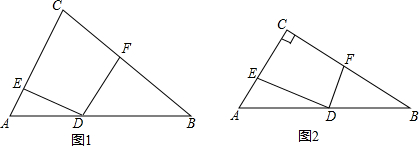
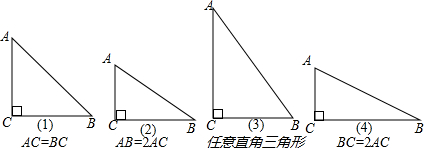
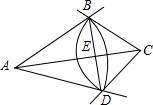如图，在△ABC中，按如下步骤作图：