题目内容
20.关于x的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在,请求出P点的坐标;若不存在,请说明理由.
分析 (1)把A和C点坐标代入y=-x2+bx+c得关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)如图,作PH⊥AD于H,先把抛物线一般式配成顶点式得到D(-1,4),E(-1,0),再利用勾股定理计算出AD,设P(-1,t),则PE=PH=t,DP=4-t,然后证明Rt△DPH∽Rt△DAE,再利用相似比得到关于t的方程,解方程求出t即可得到P点坐标.
解答 解:(1)把A(-3,0),C(0,3)代入y=-x2+bx+c得$\left\{\begin{array}{l}{-9-3b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
所以抛物线解析式为y=-x2-2x+3;
(2)存在.
如图,作PH⊥AD于H,
∵y=-x2-2x+3=-(x+1)2+4,
∴抛物线的对称轴为直线x=-1,D(-1,4),E(-1,0),
∴AD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
设P(-1,t),则PE=PH=t,DP=4-t,
∵∠PDH=∠ADE,
∴Rt△DPH∽Rt△DAE,
∴$\frac{PH}{AE}$=$\frac{DP}{DE}$,即$\frac{t}{2}$=$\frac{4-t}{2\sqrt{5}}$,解得t=$\sqrt{5}$-1,
∴P点坐标为(-1,$\sqrt{5}$-1).
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案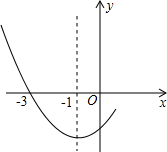 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0)下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(0,y2)是抛物线上的两点,则y1>y2.其中说法正确的是( )| A. | ①② | B. | ②③ | C. | ①②④ | D. | ②③④ |
| A. | 5.433×107 | B. | 5.433×106 | C. | 543.3×104 | D. | 5433×103 |
| A. | -3 | B. | -π | C. | -$\sqrt{5}$ | D. | 0 |
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |