题目内容
16.若关于x的分式方程$\frac{x+1}{x-1}-\frac{m}{{x}^{2}-1}=1$的解是负数,则m的取值范围是m<2且m≠0.分析 解该分式方程,根据方程的解为负数且不能使分母为0,可得关于m的不等式,解不等式可得.
解答 解:去分母,得:(x+1)2-m=x2-1,
去括号,得:x2+2x+1-m=x2-1,
移项、合并,得:2x=m-2,
系数化为1,得:x=$\frac{m-2}{2}$,
∵方程的解为负数,且x≠-1,
∴$\frac{m-2}{2}$<0,且$\frac{m-2}{2}$≠-1,
解得:m<2且m≠0,
故答案为:m<2且m≠0.
点评 本题主要考查解分式方程及分式方程的解、解不等式的基本技能,根据方程的解得出不等式是解题的关键,易忽略分式方程的增根的情况,要注意.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
11.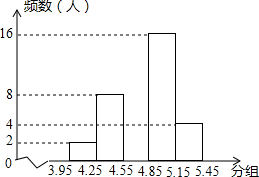 青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:
青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:
(1)根据上述数据,补全频数分布直方图和频数分布表;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市5000名初中毕业生中约有多少名学生的视力需要矫正.
 青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:
青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:| 分组 | 频数 | 频率 |
| 3.95~4.25 | 2 | 0.04 |
| 4.25~4.55 | 8 | 0.16 |
| 4.55~4.85 | 20 | 0.40 |
| 4.85~5.15 | 16 | 0.32 |
| 5.15~5.45 | 4 | 0.08 |
| 合计 | 1 |
(2)若视力在4.85以上属于正常,不需矫正,试估计该市5000名初中毕业生中约有多少名学生的视力需要矫正.
8.将左图案剪成若干小块,再分别平移后能够得到①、②、③中的( )


| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.x为何值时,$\frac{x}{x-1}$在实数范围内有意义( )
| A. | x>1 | B. | x≥1 | C. | x≠1 | D. | x≤0 |
6.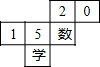 一个正方体的展开图如图所示,将它折成正方体后,数字“0”的对面是( )
一个正方体的展开图如图所示,将它折成正方体后,数字“0”的对面是( )
 一个正方体的展开图如图所示,将它折成正方体后,数字“0”的对面是( )
一个正方体的展开图如图所示,将它折成正方体后,数字“0”的对面是( )| A. | 数 | B. | 5 | C. | 1 | D. | 学 |
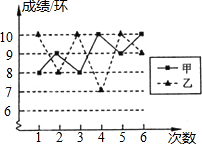 射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.
射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.
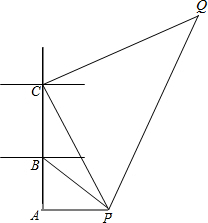 如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.
如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.