题目内容
11.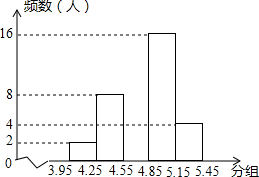 青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:
青少年视力水平下降已引起全社会的广泛关注,为了了解某市5000名初中毕业生的视力情况.我们从中抽取了一部分学生的视力作为样本进行数据处理,得到如下的频数分布表和频数分布直方图:| 分组 | 频数 | 频率 |
| 3.95~4.25 | 2 | 0.04 |
| 4.25~4.55 | 8 | 0.16 |
| 4.55~4.85 | 20 | 0.40 |
| 4.85~5.15 | 16 | 0.32 |
| 5.15~5.45 | 4 | 0.08 |
| 合计 | 1 |
(2)若视力在4.85以上属于正常,不需矫正,试估计该市5000名初中毕业生中约有多少名学生的视力需要矫正.
分析 (1)用某一组的频数除以该组的频率即可得到样本容量,乘以其频率即可得到该组的频数;
(2)用该市的总学生数乘以视力在4.85以下的频率即可.
解答 解:(1)∵第一小组的频数为2,频率为0.04,
∴样本容量为:2÷0.04=50人,
∴4.25~4.55的频率为8÷50=0.16;
4.55~4.85小组的频数为:50×0.4=20;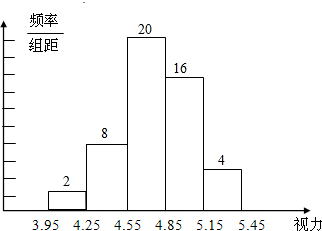
(2)视力在4.85以上的频率之和为:0.32+0.08=0.4,
5000×0.4=2000
因此该市5000名初中毕业生中约有2000名学生的视力需要矫正.
点评 本题考查了频数分布图和频率分布直方图的知识,根据频率、频数及样本容量之间的关系进行正确的运算是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
3.在代数式$\frac{{x}^{2}}{x}$、$\frac{1}{2}$、$\frac{{x}^{2}+1}{2}$、$\frac{3xy}{π}$、$\frac{3}{x+y}$、a+$\frac{1}{m}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.计算(am)3•an的结果是( )
| A. | a${\;}^{{m}^{2}+n}$ | B. | a3m+n | C. | a3(m+n) | D. | a3mn |
1.如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n=( )
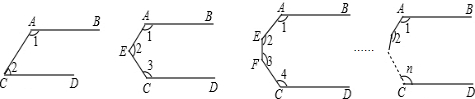

| A. | n•180° | B. | 2n•180° | C. | (n-1)•180° | D. | (n-1)2•180° |