题目内容
行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得数据如下表:
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
| 刹车时车速/km•h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
考点:二次函数的应用
专题:
分析:(1)依题意描点连线即可.
(2)设抛物线为y=ax2+bx+c,再根据表格中所给数据可得方程
,解出a,b,c即可.
(3)当y=46.5时,代入函数关系式解出x的值,根据题意进行取舍即可.
(2)设抛物线为y=ax2+bx+c,再根据表格中所给数据可得方程
|
(3)当y=46.5时,代入函数关系式解出x的值,根据题意进行取舍即可.
解答:解:(1)如图所示: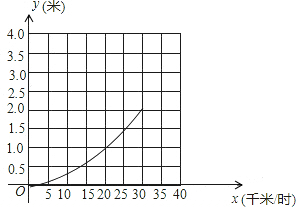
(2)根据图象可估计为抛物线.
∴设y=ax2+bx+c.
把表内前三对数代入函数,可得
,
解得:
,
∴y=0.002x2+0.01x.
经检验,其他各数均满足函数(或均在函数图象上);
(3)当y=46.5时,46.5=0.002x2+0.01x.
整理可得x2+5x-23250=0.
解之得x1=150,x2=-155(不合题意,舍去).
所以可以推测刹车时的速度为150千米/时.
∵150>140,
∴汽车发生事故时超速行驶.

(2)根据图象可估计为抛物线.
∴设y=ax2+bx+c.
把表内前三对数代入函数,可得
|
解得:
|
∴y=0.002x2+0.01x.
经检验,其他各数均满足函数(或均在函数图象上);
(3)当y=46.5时,46.5=0.002x2+0.01x.
整理可得x2+5x-23250=0.
解之得x1=150,x2=-155(不合题意,舍去).
所以可以推测刹车时的速度为150千米/时.
∵150>140,
∴汽车发生事故时超速行驶.
点评:本题考查了待定系数法求函数的解析式的运用,点的坐标的求法及运用二次函数解决实际问题的应用,解答是求出函数的解析式是关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
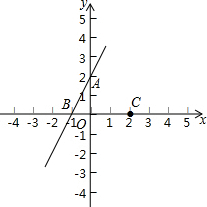 如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0). 如图,以等腰Rt△ABC的直角顶点A作两个同心圆,大圆过B、C两点,小圆与斜边BC相切于点D,若圆环(图中阴影部分)的面积为16πcm2,则AB=
如图,以等腰Rt△ABC的直角顶点A作两个同心圆,大圆过B、C两点,小圆与斜边BC相切于点D,若圆环(图中阴影部分)的面积为16πcm2,则AB=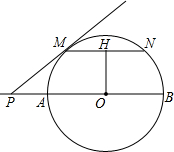 如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求:
如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求: