题目内容
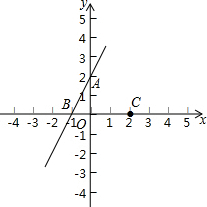 如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(2,0).(1)求直线AB的函数表达式;
(2)直线AB上有一点P,使得△PBC的面积等于9,求点P的坐标;
(3)设点D与A、B、C点构成平行四边形,直接写出所有符合条件的点D的坐标.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)根据三角形的面积公式,可得方程,根据解一元一次方程,可得答案;
(3)根据两组对边分别相等的四边形是平行四边形,可得答案.
(2)根据三角形的面积公式,可得方程,根据解一元一次方程,可得答案;
(3)根据两组对边分别相等的四边形是平行四边形,可得答案.
解答:解:(1)设直线AB的函数解析式为y=kx+b,
∵直线AB经过点A(0,2)、B(-1,0),得
,
解得
.
∴直线AB的函数解析式为y=2x+2;
(2)由题意,设点P的坐标为(x,2x+2),
S△POA=
×BC×|py|=
×3×|2x+2|=9.
解得x=2或x=-4.
故点P的坐标是(2,6)或(-4,-6);
(3)当AD=BC,AB=DC时,AD=BC=3,D(3,2);
当AD=BC,BD=AC时,AD=BC=3,D(-3,2)
当AC=BD,AB=DC时,D(1,-2);
综上所述:点D与A、B、C点构成平行四边形,点D的坐标为(3,2)、(-3,2)、(1,-2).
∵直线AB经过点A(0,2)、B(-1,0),得
|
解得
|
∴直线AB的函数解析式为y=2x+2;
(2)由题意,设点P的坐标为(x,2x+2),
S△POA=
| 1 |
| 2 |
| 1 |
| 2 |
解得x=2或x=-4.
故点P的坐标是(2,6)或(-4,-6);
(3)当AD=BC,AB=DC时,AD=BC=3,D(3,2);
当AD=BC,BD=AC时,AD=BC=3,D(-3,2)
当AC=BD,AB=DC时,D(1,-2);
综上所述:点D与A、B、C点构成平行四边形,点D的坐标为(3,2)、(-3,2)、(1,-2).
点评:本题考查了一次函数的综合题,利用了待定系数法求函数解析式,三角形的面积公式,平行四边形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
单项式-xy2z3的系数及次数分别是( )
| A、系数是0,次数是5 |
| B、系数是1,次数是6 |
| C、系数是-1,次数是5 |
| D、系数是-1,次数是6 |
 如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花
如图,正方形的棱长为3厘米,把所有的面分成3×3个小正方形,起边长都为1厘米,若一只蚂每秒爬行2.5厘米,则它下底面A点沿表面爬行至右侧面B点,最少要花 如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.