题目内容
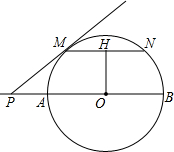 如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求:
如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求:(1)直径AB的长;
(2)AP的长.
考点:切线的性质
专题:计算题
分析:(1)连接OM,如图,由OH⊥MN,根据垂径定理得MH=
MN=3,然后在Rt△OHM中利用勾股定理可计算出OM=5,则AB=10;
(2)根据切线的性质∠OMP=90°,再证明Rt△POM∽Rt△OMH,利用相似比可计算出PO,然后利用PA=OP-OA求解.
| 1 |
| 2 |
(2)根据切线的性质∠OMP=90°,再证明Rt△POM∽Rt△OMH,利用相似比可计算出PO,然后利用PA=OP-OA求解.
解答: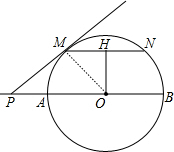 解:(1)连接OM,如图,
解:(1)连接OM,如图,
∵OH⊥MN,
∴MH=NH=
MN=3,
在Rt△OHM中,∵OH=4,MH=3,
∴OM=
=5,
∴AB=10;
(2)∵PM为⊙O的切线,
∴OM⊥PM,
∴∠OMP=90°,
∵MN∥AB,
∴∠POM=∠OMH,
∴Rt△POM∽Rt△OMH,
∴
=
,即
=
,
∴PO=
,
∴PA=OP-OA=
-5=
.
 解:(1)连接OM,如图,
解:(1)连接OM,如图,∵OH⊥MN,
∴MH=NH=
| 1 |
| 2 |
在Rt△OHM中,∵OH=4,MH=3,
∴OM=
| OH2+MH2 |
∴AB=10;
(2)∵PM为⊙O的切线,
∴OM⊥PM,
∴∠OMP=90°,
∵MN∥AB,
∴∠POM=∠OMH,
∴Rt△POM∽Rt△OMH,
∴
| PO |
| OM |
| OM |
| MH |
| PO |
| 5 |
| 5 |
| 3 |
∴PO=
| 25 |
| 3 |
∴PA=OP-OA=
| 25 |
| 3 |
| 10 |
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和相似三角形的判定与性质.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )
如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )| A、60° | B、70° |
| C、80° | D、140° |
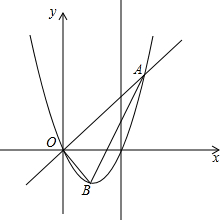 如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3
如图,已知直线y=x与二次函数y=x2+bx的图象交于点A、O,(O是坐标原点),点B为二次函数图象的顶点,OA=3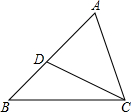 如图,△ABC中,D是AB上的一点,△ABC∽△ACD,且AD:AC=3:4,∠ADC=65°,∠B=43°.
如图,△ABC中,D是AB上的一点,△ABC∽△ACD,且AD:AC=3:4,∠ADC=65°,∠B=43°.