题目内容
1.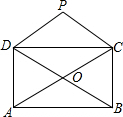 如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.
如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.(1)求证:四边形OCPD是菱形;
(2)若∠ACD=30°,菱形OCPD的面积为9$\sqrt{3}$,求AC的长;
(3)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形OCPD是矩形.
分析 (1)由PD∥AC,PC∥BD,易得四边形OCPD是平行四边形,又由矩形ABCD的对角线互相平分且相等,即可得OC=OD,继而证得四边形OCPD是菱形;
(2)由四边形OCPD是菱形;易得S菱形OCPD=S△ADC,又由∠ACD=30°,菱形OCPD的面积为9$\sqrt{3}$,即可求得答案;
(3)由PD∥AC,PC∥BD,易得四边形OCPD是平行四边形,又由菱形的对角线互相垂直,即可得AC⊥BD,继而证得四边形OCPD是矩形.
解答 (1)证明:∵PD∥AC,PC∥BD,
∴四边形OCPD是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OD=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AC,
∴OC=OD,
∴四边形OCPD是菱形;
(2)解:∵四边形OCPD是菱形;
∴S△OCD=S△PCD,
∵OA=OC,
∴S△OCD=S△OAD,
∴S△OAD=S△PCD,
∴S菱形OCPD=S△ADC,
∵∠ACD=30°,
∴AD=$\frac{1}{2}$AC,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{3}$AD,
∴$\frac{1}{2}$AD•$\sqrt{3}$AD=9$\sqrt{3}$,
解得:AD=3$\sqrt{2}$,
∴AC=6$\sqrt{2}$;
(3)矩形.
证明:∵PD∥AC,PC∥BD,
∴四边形OCPD是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCPD是矩形.
故答案为:矩.
点评 此题考查了矩形的性质与判定、菱形的判定与性质以及含30°的直角三角形的性质.注意掌握菱形的对角线互相垂直以及矩形的对角线互相平分且相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.±3是9的( )
| A. | 平方根 | B. | 相反数 | C. | 绝对值 | D. | 算术平方根 |
7.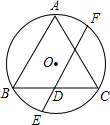 如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
 如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )| A. | $\sqrt{5}$+1 | B. | 2$\sqrt{5}$-2 | C. | 2$\sqrt{3}$-2 | D. | $\sqrt{3}$+1 |
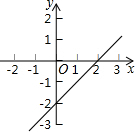 如图所示,是函数y=kx+b的图象,利用图象解答:
如图所示,是函数y=kx+b的图象,利用图象解答: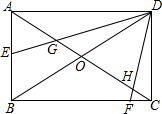 已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$.
已知:如图,在矩形ABCD中,∠EDF两边分别与边AB、BC交于E、F,与对角线交于G、H,且∠EDF=∠BDC,∠BDC=60°,AE=2,DH=$\sqrt{13}$时,DG=$\frac{4\sqrt{13}}{3}$. 小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )
小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )